静安区风华初级中学初二（上）数学第二次月考考试试题
（满分100分，考试时间90分钟）
1、选择题：（本大题共6题，每题3分，满分18分）
1.下列方程中，是一元二次方程的是………………………………………（ ）
（A）a
+bx+c=0 （B）2 -4 =
（C）x（2x-1）=2 （D）
=0
2.下列图像中表示y是x的函数的是……………………………………（ ）
（A） （B） （C） （D）
3.下列各组的两个变量之间，成正比率的是…………………………（ ）
（A）矩形的面积和它的一条边长 （B） 圆的半径的它的面积
（C）工作效率肯定，工作量与工作时间 （D）路程肯定，速度与时间
4.下列函数（其中x是自变量）中，是正比率函数的是……………（ ）
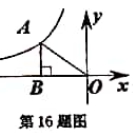
（A）y= （B）y=（ 
）x
（C）y=
x+1 （D）y=
5.正比率函数y=kx和反比率函数y=
（k是常数且k≠0）在同一平面直角坐标系中的图形可能是………………………………………………（ ）
6.下列命题的逆命题是真命题的是……………………………………（ ）
（A）两直线平行，同位角相等 （B）对等角相等
（C）若a=b,则
=
（D）若（a+1）x＞a+1,则x＞1
2、填空题（本大题共12题，每题3分，满分36分）
7.不等式2x＞
x+3 的解集是__________.
8.已知关于x的一元二次方程k-6x-1=0有两个实数根，则k的取值范围是__________.__________
9.函数y=
的概念域是__________.
10.已知f（x）=
,则f（）=__________.
11.假如函数y=2x的自变量x取值范围是-3＜x＜0，那样y的取值范围是__________.
12.已知函数y=（2a-3）x的函数经过2、四象限，则a的取值范围是__________.
13.若函数y=（m-2）
是反比率函数，则m=__________.
14.下列函数：①y=3x ②y=-3x ③y= - 
④y=
中，y随x的减小而减小的有__________.
15.已知直线y=kx与双曲线y=
交于M、N点，点M的横坐标是2，写出正比率函数的分析式__________.
16.如图，点A为反比率函数y=
图像上一点，AB垂直x轴于B，若S△AOB=3，则k的值为__________.
17.有一群马上毕业的大四学生在一块聚会，每两个人之间互送照片，共送出132张，那样这群大四学生中有多少人。假如设这群大四学生工有x人，那样依据题意可列一元二次方程是__________.
18.某工厂7月份的产值是200万元，计划9月份的产值要达到288元，那样平均每月的增长率是__________.
3、简答卷（本大题共4题，第19-21题每题5分，第22、23题每题6分，满分27分）
19.用配办法解方程：4-2x-1=0 20.在实数范围内因式分解：-2xy -4
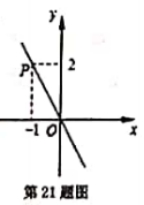
21.如图，正比率函数的图像经过点P和点Q（-m ，m+3）,求m的值.
22.已知y=
+
,
与x+1成正比率，与x成反比率，且当x=1时，y=5，当x=-1时，y=-1，求y与x之间的函数分析式.
23.下面的图像反映的过程是：张强从家跑步去体育场，在哪儿训练了一阵后又原路返回，顺路到文具店去买笔，然后散步回家.其中x表示时间，y表示张强离家的距离。依据图形回答：
（1）体育场离张强家__________千米，
张强从家到体育场共用了__________分钟；
（2）体育场离文具店__________千米；
（3）张强在文具店逗留了__________分钟.
4、解答卷（本大题共3题，第24、25每题6分，第26题7分，共19分）
24.风华初级中学马上举行元旦汇演，演出前筹备借助26米长的墙为一边，用48米隔栏绳为三变=边，设立一个面积为300平米的长方形演员等候区。如图，为了便捷演员进出，在两边空出两个各为1米的出入口，问围成的这个长方形的相邻两边的长分别是多少米？
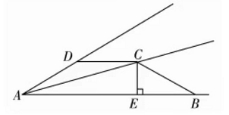
25.四边形ABCD中，AC平分∠BAD，CE⊥AB于E，∠ADC+∠CBE=180°，求证：2AE=AB+AD.
26.如图，在平面直角坐标系中，点A（4,0），点B（0,6），点P是直线AB上的一个动点，已知点P的坐标为（m,n）.
当点P在线段AB上时（不与点A、B重合）
①当m=2,n=3时，求△POA的面积.
②记△POB的面积为S，求S关于m的函数分析式，并写出概念域.
（2）假如S△BOP：S△POA=1:2,请直接写出直线OP的函数分析式.（本小题只须写出结果，无需写出解题过程）.
