第一章有理数
1.有理数:
凡能写成![]() 形式的数,都是有理数,整数和分数统称有理数.
形式的数,都是有理数,整数和分数统称有理数.
注意:0即不是正数,更不是负数;-a可能不是负数,+a也可能不是正数;p不是有理数;
有理数的分类: ① 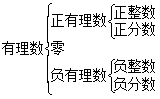 ②
② 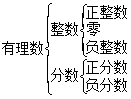
注意:有理数中,1、0、-1是三个特殊的数,它们有我们的特质;这三个数把数轴上的数分成四个地区,这四个地区的数也有我们的特质;
自然数Û 0和正整数; a>0 Û a是正数; a<0 Û a是负数;
a≥0 Û a是正数或0 Û a是非负数; a≤ 0 Û a是负数或0 Û a是非正数.
2.数轴:数轴是规定了原点、正方向、单位长度(数轴的三要点)的一条直线.
3.相反数:只有符号不一样的两个数,大家说其中一个是另一个的相反数;0的相反数还是0; 注意: a-b+c的相反数是-= -a+b-c;a-b的相反数是b-a;a+b的相反数是-a-b;
相反数的和为0 Û a+b=0 Û a、b互为相反数.
相反数的商为-1.
(5)相反数的绝对值相等______________________________
4.绝对值:
正数的绝对值等于它本身,0的绝对值是0,负数的绝对值等于它的相反数;
注意:绝对值的意义是数轴上表示某数的点离开原点的距离;
绝对值可表示为: 或
或 ![]() ;
;
![]() ;
; ![]() ;
;
|a|是要紧的非负数,即|a|≥0,非负性;
5.有理数比大小:
(1)正数永远比0大,负数永远比0小;
(2)正数大于所有负数;
(3)两个负数比较,绝对值大的反而小;
(4)数轴上的两个数,右侧的数总比左侧的数大;
(5)-1,-2,+1,+4,-0.5,以上数据表示与标准水平的差,绝对值越小,越接近标准。
6.倒数:乘积为1的两个数互为倒数;
注意:0没倒数; 若ab=1Û a、b互为倒数; 若ab=-1Û a、b互为负倒数.
等于本身的数大全:
相反数等于本身的数:0
倒数等于本身的数:1,-1
绝对值等于本身的数:正数和0
平方等于本身的数:0,1
立方等于本身的数:0,1,-1.
7. 有理数加法法则:X|k |b| 1 . c|o |m
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值;
(3)一个数与0相加,仍得这个数.
8.有理数加法的运算律:
(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b)+c=a+(b+c).
9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b).
10 有理数乘法法则:(1)两数相乘,同号得正,异号得负,并把绝对值相乘;
(2)任何数与零相乘都得零;
(3)几个因式都不为零,积的符号由负因式的个数决定.奇数个负数为负,偶数个负数为正。
11 有理数乘法的运算律:
(1)乘法的交换律:ab=ba;(2)乘法的结合律:(ab)c=a(bc);
(3)乘法的分配律:a(b+c)=ab+ac .(方便运算)
12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不可以做除数,![]() .
.
13.有理数乘方的法则:(1)正数的任何次幂都是正数;
(2)负数的奇次幂是负数;负数的偶次幂是正数;
14.乘方的概念:(1)求相同因式积的运算,叫做乘方;
(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;
(3)a2是要紧的非负数,即a2≥0;若a2+|b|=0 Û a=0,b=0;
(4)正数的任何次幂都是正数,0的任何次幂都是0;负数的奇次幂是负数,负数的偶次幂是正数。
(5)据规律 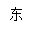 底数的小数点移动一位,平方数的小数点移动二位.
底数的小数点移动一位,平方数的小数点移动二位.
15.科学记数法:把一个大于10的数记成a×10n的形式,其中a是整数数位只有一位的数即1≤a<10,这种记数法叫科学记数法.10的指数=整数位数-1, 整数位数=10的指数+1
16.近似数的精准位:一个近似数,四舍五入到哪一位,就说这个近似数精准到那一位.
17.混合运算法则:先乘方,后乘除,最后加减; 注意:不省过程,不跳步骤。
18.特殊值法:是用符合题目需要的数代入,并验证题设成立而进行猜想的一种办法,但不可以用于证明.常用于填空,选择。
第二章 整式的加减
1.单项式:表示数字或字母乘积的式子,单独的一个数字或字母也叫单项式。
2.单项式的系数与次数:单项式中的数字因数,称单项式的系数(要包含前面的符号);
单项式中所有字母指数的和,叫单项式的次数(只与字母有关)。
3.多项式:几个单项式的和叫多项式。 X k b 1 . c o m
4.多项式的项数与次数:多项式中所含单项式的个数就是多项式的项数,每一个单项式叫多项式的项;多项式里,次数最高项的次数叫多项式的次数;
5. (整式是代数式,但代数式可能不是整式)。
(整式是代数式,但代数式可能不是整式)。
6.相同种类项:所含字母相同,并且相同字母的指数也相同的项叫做相同种类项(与系数无关,与字母的排列顺序无关)。
7.合并相同种类项法则:系数相加,字母与字母的指数不变.
8.去(添)括号法则:去(添)括号时,若括号前边是“+”号,括号里的各项都不变号; 若括号前边是“-”号,括号里的各项都要变号.
9.整式的加减:一找:(标记);二“+”(务必用+号开始合并)三合:(合并)
10.多项式的升幂和降幂排列:把一个多项式的各项按某个字母的指数从小到大(或从大到小)排列起来,叫做按这个字母的升幂排列(或降幂排列)。
第三章 一元一次方程
1.等式:用“=”号连接而成的式子叫等式.
2.等式的性质:
等式性质1:等式两边都加上(或减去)同一个数(或式子),结果仍相等;
等式性质2:等式两边都乘以(或除以)同一个不为零的数,结果仍相等.
3.方程:含未知数的等式,叫方程(方程是含有未知数的等式,但等式可能不是方程).
4.方程的解:使等式左右两边相等的未知数的值叫方程的解;注意:“方程的解就能代入”。
5.移项:把等式一边的某项变号后移到另一边叫移项.移项的依据是等式性质1(移项变号).
6.一元一次方程:只含有一个未知数,并且未知数的次数是1,并且含未知数项的系数不是零的整式方程是一元一次方程.
7.一元一次方程的规范形式: ax+b=0(x是未知数,a、b是已知数,且a≠0).
8.一元一次方程解法的一般步骤:
化简方程----------分数基本性质
去 分 母----------同乘(不漏乘)最简公分母
去 括 号----------注意符号变化
移 项----------变号(留下靠前)
合并相同种类项--------合并后符号__________________________________________________
系数化为1---------除前面
10.列一元一次方程解应用题:
(1)读题剖析法:………… 多用于“和,差,倍,分问题”
仔细读题,找出表示相等关系的关键词,比如:“大,小,多,少,是,共,合,为,完成,增加,降低,配套-----”,借助这类关键词列出文字等式,并且据题意设出未知数,最后借助题目中的量与量的关系填入代数式,得到方程.
(2)画图剖析法: ………… 多用于“行程问题”
借助图形剖析数学问题是数形结合思想在数学中的体现,仔细读题,根据题意画出有关图形,使图形各部分具备特定的意思,通过图形找相等关系是解决问题的重点,从而获得布列方程的依据,最后借助量与量之间的关系(可把未知数看做已知量),填入有关的代数式是获得方程的基础.
11.列方程解应用题的常用公式:
(1)行程问题: 路程=速度·时间 ![]()
![]() ;
;
(2)工程问题:工作量=工作效率·工作时间 ![]()
![]() ;
;
工程问题常用等量关系: 先做的+后做的=完成量______________________________
(3)顺水逆水问题:
顺流速度=静水速度+水流速度,逆流速度=静水速度-水流速度;
顺水逆水问题常用等量关系: 顺水路程=逆水路程
(4)产品收益问题: 价格=定价![]() ,
, ![]() ;
;
收益问题常用等量关系: 价格-进价=收益
(5)配套问题:
(6)分配问题
第四章 图形初步认识
(一)多姿多彩的图形
![]() 立体图形:棱柱、棱锥、圆柱、圆锥、球等.
立体图形:棱柱、棱锥、圆柱、圆锥、球等.
1、几何图形
平面图形:三角形、四边形、圆、多边形等.
![]() 主视图---------从正面看
主视图---------从正面看
2、几何体的三视图 左视图---------从左侧看
俯瞰图---------从上面看
(1)会判断简单物体(棱柱、圆柱、圆锥、球)的三视图.
(2)能依据三视图描述基本几何体或实物原型.
3、立体图形的平面展开图
(1)同一个立体图形按不一样的方法展开,得到的平现图形不同的.
(2)知道直棱柱、圆柱、圆锥、的平面展开图,能依据展开图判断和制作立体模型.
4、点、线、面、体
(1)几何图形的组成
点:线和线相交的地方是点,它是几何图形最基本的图形.
线:面和面相交的地方是线,分为直线和曲线.
面:包围着体的是面,分为平面和曲面.
体:几何体也简称体.
(2)点动成线,线动成面,面动成体.
(二)直线、射线、线段
1、基本定义
名字 | 直线 | 射线 | 线段 |
图形
|
|
|
|
端点个数 | 无 | 一个 | 两个 |
表示法 | 直线a 直线AB(BA) | 射线a 射线AB | 线段a 线段AB(BA) |
作法叙述 | 作直线a 作直线AB; | 作射线a 作射线AB | 作线段a; 作线段AB; 连接AB |
延长 | 向两端无限延长 | 向一端无限延长 | 不可延长 |
2、直线的性质
经过两点有一条直线,并且只有一条直线.简单地:两点确定一条直线.
3、画一条线段等于已知线段
(1)度量法
(2)用尺规作图法
4、线段的长短比较办法
(1)度量法
(2)叠合法
(3)圆规截取法
5、线段的中点(二等分点)、三等分点、四等分点等
概念:把一条线段平均分成两条相等线段的点.
图形:
![]()
A M B
符号:若点M是线段AB的中点,则AM=BM=![]() AB,AB=2AM=2BM.
AB,AB=2AM=2BM.
6、线段的性质
两点的所有连线中,线段最短.简单地:两点之间,线段最短.
7、两点的距离
连接两点的线段的长度叫做两点的距离(距离是线段的长度,而不是线段本身).
8、点与直线的地方关系
(1)点在直线上(或者直线经过点) (2)点在直线外(或者直线不经过点).
(三)角
1、角:有公共端点的两条射线所组成的图形叫做角.
2、角的表示法(四种):
表示办法 |
| 记法 | 适用范围 |
用三个大写字母表示 |
| ÐAOB或ÐBOA | 任何状况下都适应。表示端点的字母需要写在中间。 |
用一个大写字母表示 |
| ÐA | 以这个点为顶点的角只有一个。 |
用数字表示 |
| Ð1 | 任何状况下都适用。但需要在挨近顶点处加上弧线表示角的范围,并注上数字或希腊字母。 |
用希腊字母表示 |
| Ða |
3、角的度量单位及换算(度”°”、分”¢”、秒”²”)60进制
1°=60¢=3600², 1¢=60²; 1¢=°, 1²=¢=°
4、角的分类
∠β | 锐角 | 直角 | 钝角 | 平角 | 周角 |
范围 | 0<∠β<90° | ∠β=90° | 90°<∠β<180° | ∠β=180° | ∠β=360° |
5、角的比较办法
(1)度量法
(2)叠合法
6、角的四则运算
角的和、差、倍、分及其近似值
7、画一个角等于已知角
(1)借用三角尺能画出15°的倍数的角,在0~180°之间共能画出11个角.
(2)借用量角器能画出给定度数的角.
(3)用尺规作图法.
8、角的平分线
概念:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做角的平分线(若OB是ÐAOC的平分线,则ÐAOB=ÐBOC=![]() ÐAOC, ÐAOC=2ÐAOB =2ÐBOC).
ÐAOC, ÐAOC=2ÐAOB =2ÐBOC).
9、互余、互补
(1)若∠1+∠2=90°,则∠1与∠2互为余角.其中∠1是∠2的余角,∠2是∠1的余角.
(2)若∠1+∠2=180°,则∠1与∠2互为补角.其中∠1是∠2的补角,∠2是∠1的补角.

![]() (3)∠1的余角可以用90°-∠1表示;∠1的补角可以用180°-∠1表示.
(3)∠1的余角可以用90°-∠1表示;∠1的补角可以用180°-∠1表示.
![]()
![]() (4)余角的性质:同角的余角相等;
(4)余角的性质:同角的余角相等;
![]() 补角的性质:同角的补角相等.
补角的性质:同角的补角相等.
![]()
![]() 10、方向角
10、方向角
(1)正方向

![]()
![]() (2)南或北写在前面,东或西写在后面
(2)南或北写在前面,东或西写在后面
![]()
![]()
![]()
![]()
![]()
![]()






