整式的乘法与因式分解
1、填空题
因式分解：
______．
计算：
______ ．
已知
，
，则
______ ．
若
，则代数式
的值为______．
若
，
，则 ______ ．
若整式
为不等于零的常数
能在有理数范围内因式分解，则k的值可以是______
写出一个即可．
2、选择题
计算的结果是
A. 
B. 
C. 
D.
下列计算中，正确的是
A. B. 
C. D. 
运用乘法公式计算
的结果是
A. 
B. C. 
D. 
将下列多项式因式分解，结果中不含有因式的是
A. 
B.
C. 
D. 
下列运算正确的是
A. 
B. 
C. 
D.
把分解因式得
A. 
B. C. D. 
若
是一个完全平方法，则
A. 20 B. 
C. 
D. 
将图甲中阴影部分的小长方形变换到图乙地方，依据两个图形的面积关系得到的数学公式是
 |
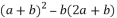A. 
B. 
C. D.
的计算结果是
A. 1 B. 
C. 2 D. 
将代数式化成的形式
A. B. 
C. 
D.
3、计算题（本大题共2小题，共12.0分）
当，时，求
的值．
阅读材料：求
的值．
解：设，将等式两边同时乘2得：
将下式减去上式得
即
即
请你仿照此法计算：其中n为正整数．
4、解答卷（本大题共5小题，共34.0分）
计算：
分解因式：
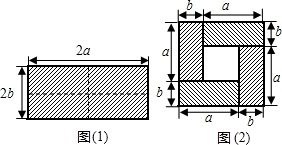
如图，是一个长为2a宽为
的矩形，用剪刀沿矩形的两条对角轴剪开，把它分成四个全等的小矩形，然后按图拼成一个新的正方形，求中间空白部分的面积用含a、b的式子表示
| |
方便计算：．
已知
，求代数式
的值．
答案
1. 
2. 
3. 4. 2 5. 8 6.
7-16. CACCD ACCAC
17. 解：当，时，原式．
18. 解：设，
将等式两边同时乘2得：
，
将下式减去上式得：
，即，
则
；设，
两边同时乘3得：
，
得：，即，
则．
19. 解：原式
．
20. 解： 
．
21. 解：由题意可得，正方形的边长为，故正方形的面积为，
原矩形的面积为4ab，
空白部分的面积
正方形的面积
矩形的面积．
22. 解： 
．
23. 解：
．，原式
．
