22.3 实质问题与二次函数 同步测试
1、选择题
1.某商品拿货单价为90元,按100元一件供应时,能售出500件.若每件涨价1元,则销量就降低10件.则该商品能获得的最大收益为()
A.5000元 B. 8000元 C. 9000元 D. 10000元
2.某旅游社有100张床位,每床每晚收费10元时,客床可全部租出,若每床每晚收费提升2元,则降低10
张床位的租出;若每床每晚收费再提升2元,则再降低10张床位租出,以每次提升2元的这种办法变化下去,为了投资少而获利大,每床每晚应提升
A.4元或6元 B.4元 C.6元 D.8元
3.心理学家发现,学生对定义的同意能力y和提出定义所用的时间x之间大致满足函数关系式:![]() ,y的值越大,表示同意能力越强,那样学生的同意能力达到最强时,定义提出所用的时间是.
,y的值越大,表示同意能力越强,那样学生的同意能力达到最强时,定义提出所用的时间是.
A.10分 B.30分 C.13分 D.15分
4.某广场有一喷水池,水从地面喷出,如图所示,以水平地面为x轴,出水点为原点,打造平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x的一部分,则水喷出的最大高度是
A.4米 B.3米 C.2米 D.1米

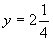
第4题 第6题
5.一小球被抛出后,距离地面的高度h和飞行时间t满足下列函数关系式:h=-52+6,则小球距离地面的最大高度是
A.1米 B.5米 C.6米 D.7米
6.某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每一个小正方形的种植策略相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG地区上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是()

A. B.
B.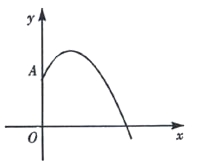 C.
C. D.
D.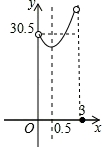
2、填空题
7.一件工艺品进价为100元,标价135元售出,天天可售出100件.依据销售统计,一件工艺品每降价1元供应,则天天可多售出4件,要使天天获得的价值最大,每件需降价的钱数为________元.
8.供应某种手工艺品,若每一个获利x元,一天可售出个,则当x=________元时,一天供应该种手工艺品的总收益y最大.
9.在平面直角坐标系xOy中,二次函数C1:y=ax2+bx+c的图象与C2:y=2x2-4x+3的图象关于y轴对称,且C1与直线y=mx+2交与点A.则m的值为__________.
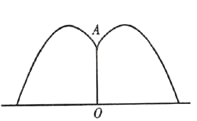
10.某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在每个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线形状如图所示,如图打造直角坐标系,水流喷出的高度![]() 与水平距离
与水平距离![]() 之间的关系式是
之间的关系式是![]() .请回答下列问题:柱子OA的高度为 __________米;喷出的水流距水平面的最大高度是__________米;若不计其它原因,水池的半径至少要__________米,才能喷出的水流不至于落在池外.
.请回答下列问题:柱子OA的高度为 __________米;喷出的水流距水平面的最大高度是__________米;若不计其它原因,水池的半径至少要__________米,才能喷出的水流不至于落在池外.

11.如图所示,小明的爸爸在相距2米的两棵树间拴了一根绳子,给小明做了一个浅易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为________米.
第11题
12.某电子商务销售一款夏天时装,进价40元/件,价格110元/件,天天销售20件,每销售一件需缴纳电子商务平台竞价开户多少钱a元(a>0).将来30天,这款时装将拓展“天天降价1元”的夏令优惠活动,即从第1天起天天的单价均比前一天降1元.通过市场调查发现,该时装单价每降1元,天天销售量增加4件.在这30天内,要使天天缴纳电子商务平台竞价开户多少钱后的价值随天数t(t为正整数)的增大而增大,a的取值范围应为______________________________.
3、解答卷
13.为了节省材料,某水产养殖户借助水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形地区,而且这三块矩形地区的面积相等.设BC的长度为xm,矩形地区ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为什么值时,y有最大值?最大值是多少?

14. 国家推行“节能减排,低碳经济”政策后,某环保节能设施生产企业的商品供不应求。若该企业的某种环保设施每月的产量维持在肯定的范围,每套商品的生产本钱不高于50万元,每套商品的价格高于90万元.已知这种设施的月产量x与每套的价格y1之间满足关系式y2=170-2x,月产量x与生产总本钱y2存在如图所示的函数关系.
直接写出y2与x之间的函数关系式;
求月产量x的范围;
当月产量x为多少时,这种设施的价值W最大?最大收益是多少?
15.某镇地点偏僻,紧急制约着经济进步,丰富的花木商品只能在当地销售,乡政府对花木商品每投资x万元,所获收益为![]() .为了响应国内西部大开发的宏伟决策,乡政府在拟定经济进步的10年规划时,拟定开发此花木商品,而开发前后可用于该项目投资的专项资金每年最多50万元.若开发该商品,在前5年中,需要每年从专项资金中拿出25万元投资修通一条公路,且5年修通.公路修通后,花木商品除在当地销售外,还可运往外地销售,运往外地销售的花木商品,每投资x万元可获收益
.为了响应国内西部大开发的宏伟决策,乡政府在拟定经济进步的10年规划时,拟定开发此花木商品,而开发前后可用于该项目投资的专项资金每年最多50万元.若开发该商品,在前5年中,需要每年从专项资金中拿出25万元投资修通一条公路,且5年修通.公路修通后,花木商品除在当地销售外,还可运往外地销售,运往外地销售的花木商品,每投资x万元可获收益![]() .
.
若不进行开发,求10年所获收益的最大值是多少?
若按此规划进行开发,求10年所获收益的最大值是多少?
依据、计算的结果,请你用一句话谈谈你的想法.
答案与分析
1、选择题
1.【答案】C;
【分析】解:设单价定为x,总收益为W,
则可得销售量为:500﹣10(x﹣100),单件收益为:(x﹣90),
由题意得,W=(x﹣90)[500﹣10(x﹣100)]=﹣10x2+2400x﹣135000=﹣10(x﹣120)2+9000,
故可得当x=120时,W获得最大,为9000元,
故选C.
2.【答案】C;
【分析】设旅游社获利为y,若每床一次提升成本2元,设提升了x次,则每床提升成本为2x元,依据题意可列 ,由于x为整数,且为了投资少而获利大,所以当x=3即2x=6时,函数取最大值,故选C.
,由于x为整数,且为了投资少而获利大,所以当x=3即2x=6时,函数取最大值,故选C.
3.【答案】C;
【分析】![]() 分时,y最大.
分时,y最大.
4.【答案】A;
【分析】![]() ,当
,当![]() 时,
时,![]() .
.
5.【答案】C;
【分析】t=1时,![]() ;
;
6.【答案】A
【分析】S△AEF=![]() AE×AF=
AE×AF=![]() x2,S△DEG=
x2,S△DEG=![]() DG×DE=
DG×DE=![]() ×1×(3﹣x)=
×1×(3﹣x)=![]() ,
,
S五边形EFBCG=S正方形ABCD﹣S△AEF﹣S△DEG=9﹣![]() x2﹣
x2﹣![]() =﹣
=﹣![]() x2+
x2+![]() x+
x+![]() ,
,
则y=4×(﹣![]() x2+
x2+![]() x+
x+![]() )=﹣2x2+2x+30,
)=﹣2x2+2x+30,
∵AE<AD,
∴x<3,
综上可得:y=﹣2x2+2x+30(0<x<3).
故选:A
2、填空题
7.【答案】5;
8.【答案】4;
【分析】![]() ,∴
,∴ ![]() 时W最大.
时W最大.
9.【答案】1;
10.【答案】![]() ;
;![]() ;2.5.
;2.5.
【分析】(1)OA高度为![]() 米.
米.
(2)当![]() 时,
时,![]() ,即水流距水平面的最大高为
,即水流距水平面的最大高为![]() 米.
米.
(3)![]()
其中![]() 不合题意,
不合题意,![]() 水池的半径至少要2.5米,才能使喷出的水流不至于落在池外.
水池的半径至少要2.5米,才能使喷出的水流不至于落在池外.
11.【答案】0.5;
【分析】如图,打造平面直角坐标系,则A,B,C.
设抛物线分析式为![]() .则
.则
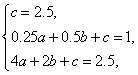 解得
解得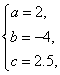
∴ ![]() ,
,
∴ 顶点坐标为,即绳子的最低点距地面0.5米.
12.【答案】0<a<6.
【分析】设将来30天天天获得的价值为y,
y=(110﹣40﹣t)(20+4t)﹣(20+4t)a
化简,得
y=﹣4t2+(260﹣4a)t+1400﹣20a
天天缴纳电子商务平台竞价开户多少钱后的价值随天数t(t为正整数)的增大而增大,
![]() ,
,
解得,a<6,
又∵a>0,即a的取值范围是:0<a<6.
3、解答卷
13.【答案与分析】
解:(1)∵三块矩形地区的面积相等,
∴矩形AEFD面积是矩形BCFE面积的2倍,
∴AE=2BE,
设BE=a,则AE=2a,
∴8a+2x=80,
∴a=﹣![]() x+10,2a=﹣
x+10,2a=﹣![]() x+20,
x+20,
∴y=(﹣![]() x+20)x+(﹣
x+20)x+(﹣![]() x+10)x=﹣
x+10)x=﹣![]() x2+30x,
x2+30x,
∵a=﹣![]() x+10>0,
x+10>0,
∴x<40,
则y=﹣![]() x2+30x(0<x<40);
x2+30x(0<x<40);
(2)∵y=﹣![]() x2+30x=﹣
x2+30x=﹣![]() (x﹣20)2+300(0<x<40),且二次项系数为﹣
(x﹣20)2+300(0<x<40),且二次项系数为﹣![]() <0,
<0,
∴当x=20时,y有最大值,最大值为300平米.
14.【答案与分析】
解:y2=500+30x.
依题意得:![]()
解之:25≤x≤40,且x为整数.
∵ ![]()
![]() ,
,
∴ ![]() ,而25<35<40.
,而25<35<40.
∴ 当x=35时,![]() 1 950.
1 950.
即月产量为35套时,收益最大,最大收益是l 950万元.
15.【答案与分析】
解:若不开发此商品,根据原来的投资方法,由![]() 知,仅需从50万元专款中拿出30万元投资,每年即可获得最大收益10万元,则10年的最大收益为M1=10×10=100.
知,仅需从50万元专款中拿出30万元投资,每年即可获得最大收益10万元,则10年的最大收益为M1=10×10=100.
若对该商品进行开发,在前5年中,当x=25时,
每年最大收益是![]() ,
,
则前5年的最大收益为M2=9.5×5=47.5.
设后5年中x万元是用于当地销售的投资.则由![]() 知,
知,
将剩下的万元全部用于外地销售的投资,才大概获得最大收益.则后5年的价值
是![]() .
.
故当x=20时,M3获得最大值为3500万元.
所以,10年的最大收益为M=M2+M3=3500+47.5=3547.5.
由于3547.5>100,故该项目有很大的开发价值.







