物理(必学一)——常识考试知识点
第一章:运动的描述
__________
时间间隔能展示运动的一个过程,时刻只能显示运动的一个瞬间。对一些关于时间间隔和时刻的表述,可以正确理解。如:
第4s末、4s时、第5s初……均为时刻;4s内、第4s、第2s至第4s内……均为时间间隔。
不同:时刻在时间轴上表示一点,时间间隔在时间轴上表示一段。
__________
位移表示地方变化,用由初地方到末地方的有向线段表示,是矢量。路程是运动轨迹的长度,是标量。只有当物体做单向直线运动时,位移的大小等于路程。通常情况下,路程≥位移的大小。
__________
| 速度 | 速率 |
物理意义 | 描述物体运动快慢和方向的物理量,是矢 量 | 描述物体运动快慢的物理量,是 标量 |
分类 | 平均速度、瞬时速度 | 速率、平均速率(=路程/时间) |
决定原因 | 平均速度由位移和时间决定 | 由瞬时速度的大小决定 |
方向 | 平均速度方向与位移方向相同;瞬时速度 方向为该质点的运动方向 | 无方向 |
联系 | 它们的单位相同(m/s),瞬时速度的大小等于速率 | |
__________
| 速度 | 加速度 | 速度变化量 |
意义 | 描述物体运动快慢和方向的物理量 | 描述物体速度变化快 慢和方向的物理量 | 描述物体速度变化大 小程度的物理量,是 一过程量 |
概念式 |
|
|
|
单位 | m/s | m/s2 | m/s |
决定原因 | v的大小由v0、a、t 决定 | a不是由v、△v、△t 决定的,而是由F和 m决定。 |
而且 由a与△t决定 |
方向 | 与位移x或△x同向, 即物体运动的方向 | 与△v方向一致 | 由
|
大小 | ① 位移与时间的比值 ② 位移对时间的变化 率 ③ x-t图象中图线 上点的切线斜率的大 小值 | ① 速度对时间的变 化率 ② 速度改变量与所 用时间的比值 ③ v—t图象中图线 上点的切线斜率的大 小值 |
|
__________
因为图象能直观地表示出物理过程和各物理量之间的关系,所以在解题的过程中被广泛应用。在运动学中,常常用到的有x-t图象和v—t图象。
理解图象的意思:
(1)x-t图象是描述位移随时间的变化规律
(2)v—t图象是描述速度随时间的变化规律
2. 明确图象斜率的意思:
x-t图象中,图线的斜率表示速度
v—t图象中,图线的斜率表示加速度
第二章:匀变速直线运动的研究
__________
基本公式:
速度—时间关系式:![]()
位移—时间关系式:![]()
位移—速度关系式:![]()
三个公式中的物理量只须了解任意三个,就可求出其余两个。
借助公式解题时注意:x、v、a为矢量及正、负号所代表的是方向的不同。
解题时要有正方向的规定。
常用推论:
平均速度公式:![]()
一段时间中间时刻的瞬时速度等于这期间内的平均速度:![]()
一段位移的中间地方的瞬时速度: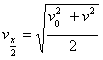
任意两个连续相等的时间间隔(T)内位移之差为常数(逐差相等):![]()
![]()
__________
研究运动图象:
从图象辨别物体的运动性质
能认识图象的截距(即图象与纵轴或横轴的交点坐标)的意义
能认识图象的斜率(即图象与横轴夹角的正切值)的意义
能认识图象与坐标轴所围面积的物理意义
能说明图象上任一点的物理意义
x-t图象和v—t图象的比较:
如图所示是形状一样的图线在x-t图象和v—t图象中,
![]()

![]()
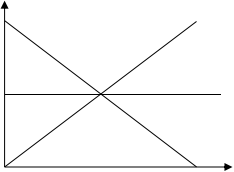
x-t图象 | v—t图象 |
①表示物体做匀速直线运动(斜率表示速度) | ①表示物体做匀加速直线运动(斜率表示加速度) |
②表示物体静止 | ②表示物体做匀速直线运动 |
③表示物体静止 | ③表示物体静止 |
④ 表示物体向反方向做匀速直线运动;初 位移为x0 | ④ 表示物体做匀减速直线运动;初速度为 v0 |
⑤ 交点的纵坐标表示三个运动的支点相遇时 的位移 | ⑤ 交点的纵坐标表示三个运动质点的一同速 度 |
⑥t1时间内物体位移为x1 | ⑥ t1时刻物体速度为v1 |
____________________
1.“追及”、“相遇”的特点:
“追及”的主要条件是:两个物体在追赶过程中处在同一地方。
两物体恰能“相遇”的临界条件是两物体处在同一地方时,两物体的速度恰好相同。
2.解“追及”、“相遇”问题的思路:
(1)依据对两物体的运动过程剖析,画出物体运动示意图
(2)依据两物体的运动性质,分别列出两个物体的位移方程,注意要将两物体的运动时间的关系反映在方程中
(3)由运动示意图找出两物体位移间的关联方程
(4)联立方程求解
剖析“追及”、“相遇”问题时应注意的问题:
抓住一个条件:是两物体的速度满足的临界条件。如两物体距离最大、最小,恰好追上或恰好追不上等;两个关系:是时间关系和位移关系。
若被追赶的物体做匀减速运动,注意在追上前,该物体是不是已经停止运动
解决“追及”、“相遇”问题的办法:
数学办法:列出方程,借助二次函数求极值的办法求解
物理办法:即通过对物理情景和物理过程的剖析,找到临界状况和临界条件,然后列出方程求解
__________
判断物体的运动性质:
依据匀速直线运动特征x=vt,若纸带上各相邻的点的间隔相等,则可判断物体做匀速直线运动。
由匀变速直线运动的推论![]() ,若所打的纸带上在任意两个相邻且相等的时间内物体的位移之差相等,则说明物体做匀变速直线运动。
,若所打的纸带上在任意两个相邻且相等的时间内物体的位移之差相等,则说明物体做匀变速直线运动。
求加速度:
逐差法:
![]()
(2)v—t图象法:
借助匀变速直线运动的一段时间内的平均速度等于中间时刻的瞬时速度的推论,求出各点的瞬时速度,打造直角坐标系(v—t图象),然后进行描点连线,求出图线的斜率k=a.
第三章 相互用途
__________
1、弹力的产生:
条件:(1)物体间是不是直接接触
(2)接触处是不是有相互挤压或拉伸
2.弹力方向的判断:
弹力的方向一直与物体形变方向相反,指向物体恢复原状的方向。弹力有哪些用途线一直通过两物体的接触点并沿其接触点公共切面的垂直方向。
重压的方向一直垂直于支持面指向被压的物体(受力物体)。
支持力的方向一直垂直于支持面指向被支持的物体(受力物体)。
绳的拉力是绳对所拉物体的弹力,方向一直沿绳指向绳缩短的方向(沿绳背离受力物体)。
补充:物体间点面接触时其弹力方向过点垂直于面,点线接触时其弹力方向过点垂直于线,两物体球面接触时其弹力的方向沿两球心的连线指向受力物体。
弹力的大小:
弹簧的弹力满足胡克定律:![]() 。其中k代表弹簧的劲度系数,仅与弹簧的材料有关,x代表形变量。
。其中k代表弹簧的劲度系数,仅与弹簧的材料有关,x代表形变量。
弹力的大小与弹性形变的大小有关。在弹性限度内,弹性形变越大,弹力越大。
__________
对摩擦力认识的四个“未必”:
摩擦力可能不是阻力
静摩擦力未必比滑动摩擦力小
静摩擦力的方向未必与运动方向共线,但肯定沿接触面的切线方向
摩擦力未必越小越好,由于摩擦力既可用作阻力,也可以作动力
静摩擦力用二力平衡来求解,滑动摩擦力用公式![]() 来求解
来求解
静摩擦力存在及其方向的判断:
存在判断:假设接触面光滑,看物体是不是发生相当运动,若发生相对运动,则说明物体间有相对运动趋势,物体间存在静摩擦力;若不发生相对运动,则没有静摩擦力。
方向判断:静摩擦力的方向与相对运动趋势的方向相反;滑动摩擦力的方向与相对运动的方向相反。
__________
1.物体受力剖析的办法:
办法
选择
2.受力剖析的顺序:
先重力,再接触力,最后剖析其他外力
3.受力剖析时应注意的问题:
剖析物体受力时,只剖析周围物体对研究对象所施加的力
受力剖析时,不要多力或漏力,注意确定每一个力的实力物体和受力物体,在力的合成和分解中,不要把实质没有的合力或分力当做是物体遭到的力
假如一个力的方向很难确定,可用假设法剖析
物体的受力状况会随运动状况的改变而改变,必要时依据学过的常识通过计算确定
受力剖析外部用途看整体,互相用途要隔离
__________
正交分解时打造坐标轴的原则:
以少分解力和容易分解力为原则,通常情况下应使尽量多的力分布在坐标轴上
一般使所需要的力落在坐标轴上
第四章 牛顿运动定律
__________
对牛顿第肯定律的理解:
揭示了物体不受外力用途时的运动规律
牛顿第肯定律是惯性定律,它指出所有物体都有惯性,惯性只与水平有关
一定了力和运动的关系:力是改变物体运动状况是什么原因,不是保持物体运动是什么原因
牛顿第肯定律是用理想化的实验总结出来的一条独立的规律,并不是牛顿第二定律的特例
当物体所受合力为零时,从运动成效上说,等于物体不受力,此时可以应用牛顿第肯定律
对牛顿第二定律的理解:
揭示了a与F、m的定量关系,尤其是a与F的几种特殊的对应关系:同时性、同向性、同体性、相对性、独立性
牛顿第二定律进一步揭示了力与运动的关系,一个物体的运动状况决定于物体的受力状况和初始状况
加速度是联系受力状况和运动状况的桥梁,无论是由受力状况确定运动状况,还是由运动状况确定受力状况,都需要出加速度
对牛顿第三定律的理解:
力一直成对出现于同一对物体之间,物体间的这对力一个是用途力,另一个是反用途力
指出了物体间的相互用途的特征:“四同”指大小相等,性质相等,用途在同一直线上,同时出现、消失、存在;“三不同”指方向不同,施力物体和受力物体不同,成效不同
__________
理想实验法
控制变量法
整体与隔离法
图形解析法
正交分解法
关于临界问题
处置的基本办法是:
依据条件变化或过程的进步,剖析引起的受力状况的变化和状况的变化,找到临界点或临界条件(更多种类见错题本)
__________
力、加速度、速度的关系:
物体所受合力的方向决定了其加速度的方向,合力与加速度的关系![]() ,合力只须不为零,无论速度是多大,加速度都不为零
,合力只须不为零,无论速度是多大,加速度都不为零
合力与速度无势必联系,只有速度变化才与合力有势必联系
速度大小怎么样变化,取决于速度方向与所受合力方向之间的关系,当二者夹角为锐角或方向相同时,速度增加,不然速度减小
关于轻绳、轻杆、轻弹簧的问题:
轻绳:
拉力的方向肯定沿绳指向绳缩短的方向
同一根绳上各处的拉力大小都相等
觉得受力形变极微,看做不可伸长
弹力可做瞬时变化
轻杆:
用途力方向未必沿杆的方向
各处用途力的大小相等
轻杆不可以伸长或压缩
轻杆遭到的弹力方法有:拉力、重压
弹力变化所需时间极短,可忽视不计
轻弹簧:
各处的弹力大小相等,方向与弹簧形变的方向相反
弹力的大小遵循![]() 的关系
的关系
弹簧的弹力不可以发生突变
关于超重和失重的问题:
物体超重或失重是物体对支持面的重压或对悬挂物体的拉力大于或小于物体的实质重力
物体超重或失重与速度方向和大小无关。依据加速度的方向判断超重或失重:加速度方向向上,则超重;加速度方向向下,则失重
物体出于完全失重状况时,物体与重力有关的现象全部消失:
①与重力有关的一些仪器如天平、台秤等不可以用
②竖直上抛的物体再也回不到地面
②杯口向下时,杯中的水也不流出







