初二(下)首次月考数学试题
1、选择题(本大题共12小题,每小题4分,共48分)
1.(4分)下列各式中,是分式的为()
A.![]() (1﹣x) B.
(1﹣x) B.![]() C.
C.![]() D.1
D.1![]()
2.(4分)分式![]() 的值为0,则a的值为()
的值为0,则a的值为()
A.1 B.﹣1 C.±1 D.0
3.(4分)下列各式正确的是()
A.![]() B.
B.![]()
C.![]() (a≠0) D.
(a≠0) D.![]()
4.(4分)能断定四边形ABCD是平行四边形的是()
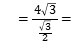
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC D.AB=AD,CB=CD
5.(4分)一个多边形,其每一个内角都是140°,则该多边形的边数是()
A.6 B.7 C.8 D.9
6.(4分)如图,在平行四边形ABCD中,AD=6,AB=4,DE平分∠ADC交BC于点E,则BE的长是()
A.2 B.3 C.4 D.5
7.(4分)如图,菱形ABCD的边长是4cm,且∠ABC=60°,E是BC中点,P点在BD上,则PE+PC的最小值为()cm.
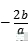
A.2 B.2![]() C.3 D.4
C.3 D.4
8.(4分)如图,点P是平行四边形ABCD内一点,已知S△PAB=7,S△PAD=4,那样S△PAC等于()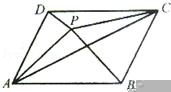
A.4 B.3.5 C.3 D.没办法确定
9.(4分)轮船在顺水航行90千米比逆水航行90千米少花了3小时,已知水流速度是2千米/时,求轮船在静水中的速度.设轮船在静水中的速度为x千米/时,依据题意列方程得()
A.![]() 3
3![]() B.
B.![]() 3
3![]()
C.![]() 2
2![]() D.
D.![]() 2
2![]()
10.(4分)对于任意的x值都有![]() ,则M,N值为()
,则M,N值为()
A.M=1,N=3 B.M=﹣1,N=3 C.M=2,N=4 D.M=1,N=4
11.(4分)如图,在平行四边形ABCD中,E,F分别是边AD,BC的中点,AC分别交BE,DF于G,H,试判断下列结论:①△ABE≌△CDF;②AG=GH=HC;③2EG=BG;④S△ABG:S四边形GHDE=2:3,其中正确的结论是()
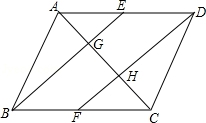
A.1个 B.2个 C.3个 D.4个
12.(4分)若整数a使关于x的不等式组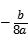 无解,且使关于x的分式方程
无解,且使关于x的分式方程![]() 2有整数解,那样所有满足条件的a值的和是()
2有整数解,那样所有满足条件的a值的和是()
A.﹣20 B.﹣19 C.﹣15 D.﹣13
2、填空题(本大题共8小题,每小题4分,共32分)
13.(4分)若一个多边形的内角和与外角和之和是1800°,则此多边形是__________边形.
14.(4分)已知![]() 5,则
5,则![]() __________.
__________.
15.(4分)若x=3是分式方程![]() 0的根,则a的值是__________.
0的根,则a的值是__________.
16.(4分)已知关于x的分式方程![]() 0有增根,则a=__________.
0有增根,则a=__________.
17.(4分)如图,△ABC中,AB=8,AC=6,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则EF为__________.
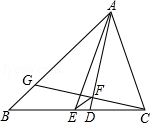
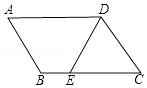
18.(4分)如图,在平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处,若△FDE的周长为12,△FCB的周长为28,则FC的长为__________.
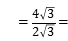
19.(4分)如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF=__________.

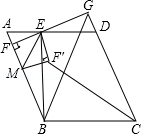
20.(4分)如图,平行四边形ABCD中,多点B作BE⊥AD于点E,过点E作EF⊥AB于点F,与CD的延长线交于点G,连接BG,且BE=BC,BG=5![]() ,∠BGF=45°,EG=3,若点M是线段BF上的一个动点,将△MEF沿ME所在直线翻折得到△MEF′,连接CF′,则CF′长度的最小值是__________.
,∠BGF=45°,EG=3,若点M是线段BF上的一个动点,将△MEF沿ME所在直线翻折得到△MEF′,连接CF′,则CF′长度的最小值是__________.
3、解答卷(共70分)
21.(10分)计算:
(1)4a2b÷(![]() )•(
)•(![]() )
)
(2)![]()
22.(10分)解分式方程
(1)![]() 1
1![]()
(2)![]()
23.(10分)在平行四边形ABCD中,分别延长BA,DC到点E,H,使得AE=AB,CH=CD,连接EH,分别交AD,BC于点F,G,求证:EF=GH.
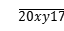
24.(10分)先化简,再求值:(![]() x﹣1)
x﹣1)![]() ,其中x是不等式组
,其中x是不等式组![]() 的整数解.
的整数解.
25.(10分)一水果店主分两批购进同一种水果,第一批所用资金为2400元,因天气缘由,水果涨价,第二批所用资金是2700元,但因为第二批单价比第一批单价每箱多10元,以致购买的数目比第一批少25%.
(1)该水果店主购进第一批这种水果每箱的单价是多少元?
(2)该水果店主计划两批水果的价格均定为每千克4元,每箱10千克,实质销售时按计划无损耗售完第一批后,发现第二批水果品质不如第一批,于是该店主将价格降低a%销售,结果还是出现了2%的损耗,但这两批水果销售完后仍赚了高于2346元,求a的最大值.
26.(10分)阅读下列材料,解决问题:
在处置分数和分式问题时,有时因为分子比分母大,或者为了分子的次数告诉于分母的次数,在实质运算时总是困难程度比较大,这个时候大家可以将假分数(分式)拆分成一个整数(或整式)与一个真分数的和(或差)的形式,通过对简单式的剖析来解决问题,大家称为离别整数法,此法在处置分式或整除问题时颇为有效,现举例说明.
材料1:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:![]() 9x+y
9x+y![]()
材料2:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母x+1,可设x2﹣x+3=(x+1)(x+a)+b
则x2﹣x+3=(x+1)(x+a)+b=x2+ax+x+a+b=x2+(a+1)x+a+b
∵对于任意x上述等式成立.
∴![]() 解得:
解得:![]() .
.
∴![]() x﹣2
x﹣2![]() .
.
如此,分式![]() 就拆分成一个整式x﹣2与一个分式
就拆分成一个整式x﹣2与一个分式![]() 的和的形式.
的和的形式.
(1)将分式![]() 拆分成一个整式与一个分子为整数的分式的和的形式,则结果为__________.
拆分成一个整式与一个分子为整数的分式的和的形式,则结果为__________.
(2)已知整数x使分式![]() 的值为整数,则满足条件的整数x=__________;
的值为整数,则满足条件的整数x=__________;
(3)已知一个六位整数![]() 能被33整除,求满足条件的x,y的值.
能被33整除,求满足条件的x,y的值.
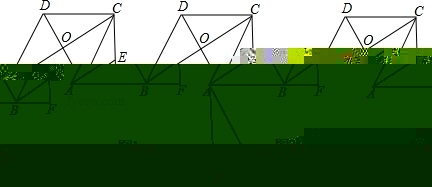
27.(10分)如图1,在菱形ABCD中,∠DAB=60°,AB=8![]() ,对角线交于点O,CF垂直AB交AB的延长线于点F,过点B作BE∥AC交FC于EF.
,对角线交于点O,CF垂直AB交AB的延长线于点F,过点B作BE∥AC交FC于EF.
(1)求BE的长:
(2)如图2,在OB上有一动点P,将△AOB绕A点顺时针旋转90°至△AOB',P点的对应点为P′,现有一动点Q从P点出发,沿着适合路径先运动到O′点,再沿O′A运动至A点,再从A点沿适合的路径运动至P′点.求Q点的最短运动路径的长;
(3)若△ABO以每秒2![]() 个单位长度的速度沿射线AB向右平移,得到三角形△A1B1O1,当A1与点F重合时停止移动,设运动时间为t,在这个过程中,点O1关于直线BC的对称点为O″,当O″,F,C三点构成的三角形为等腰三角形时,直接写出t的值.
个单位长度的速度沿射线AB向右平移,得到三角形△A1B1O1,当A1与点F重合时停止移动,设运动时间为t,在这个过程中,点O1关于直线BC的对称点为O″,当O″,F,C三点构成的三角形为等腰三角形时,直接写出t的值.
初二(下)首次月考数学试题
参考答案
1、选择题(本大题共12小题,每小题4分,共48分)
1.C; 2.B; 3.C; 4.C; 5.D; 6.A; 7.B; 8.C; 9.A; 10.B; 11.D; 12.D;
2、填空题(本大题共8小题,每小题4分,共32分)
13.__________; 14.![]() ; 15.__________; 16.__________; 17.__________; 18.__________; 19.__________; 20.
; 15.__________; 16.__________; 17.__________; 18.__________; 19.__________; 20.![]() __________;
__________;
3、解答卷(共70分)
21.【解答】解:(1)原式=4a2b•(![]() )•(
)•(![]() )
)
=b3
(2)原式![]()
![]()
![]()
22.【解答】解:(1)x=3,
(2)x![]() ,.
,.
23.【解答】证明:∵四边形ABCD为平行四边形,
∴∠BAD=∠DCB,AB=CD,AB∥CD.
∵AE=AB,CH=CD,
∴AE=CH.
∵∠EAF+∠BAD=180°,∠HCG+∠DCB=180°,∠BAD=∠DCB,
∴∠EAF=∠HCG.
∵AB∥CD,
∴∠AEF=∠CHG.
在△AEF和△CHG中,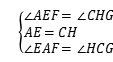 ,
,
∴△AEF≌△CHG(ASA),
∴EF=HG.
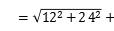
24.【解答】原式![]() .
.
25.【解答】解:(1)20元.
(2)25.
26.【解答】解:(1)答案为:x+7![]() ;
;
(2)答案为:2或4或﹣10或16;
(3)
当k=1时,x=2、y=9符合题意;
当k=2时,x=6、y=2符合题意;
当k=3时,x=9、y=5符合题意.
27.【解答】解:(1)如图1中,
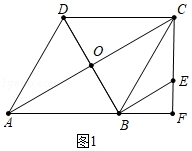
∵四边形ABCD是菱形,∠DAB=60°,
∴AB=BC=8![]() ,∠BAC=∠BCA=30°,
,∠BAC=∠BCA=30°,
∵BC∥AD,BE∥AC,
∴∠CBF=∠DAB=60°,∠BCA=∠CBE=30°,
∵CF⊥BF,
∴∠F=90°,
∴∠BCE=∠EBC=30°,
∴BE=EC,
在Rt△BCF中,BF![]() BC=4
BC=4![]() ,
,
在Rt△BEF中,cosplay30°![]() ,
,
∴BE![]() 8.
8.
(2)如图2中,
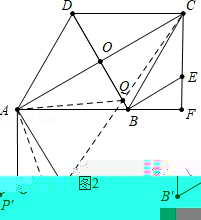
∵四边形ABCD是菱形,
∴AC⊥BDOA=OC,
∴A、C关于BD对称,
连接CO′交BD于Q,连接AQ,此时Q点的最短运动路径最短,
最短路径=QO′+O′A+AP′=CQ+QO′+AO=CO′+AO′![]() 12=12
12=12![]() 12.
12.
(3)①如图3中,当点B1与F重合时,点O1在BC的中点,易知AA1![]() AB=4
AB=4![]() ,
,
∴t![]() 2s.
2s.
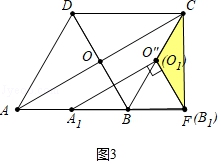
②如图4中,当FC=FO″时,设FO″交BC于H,易证四边形HO1B1F是平行四边形,
FH![]() BC=4
BC=4![]() ,HO″=HO1=B1F=12﹣4
,HO″=HO1=B1F=12﹣4![]() ,
,
∴AA1=12,t![]() 2
2![]() s.
s.
③如图5,当点A1与F重合时,CF=CO″,此时AA1=12![]() ,t=6s.
,t=6s.

综上所述,当t=2或2![]() 或6s时,△CFO″是等腰三角形.
或6s时,△CFO″是等腰三角形.







