![]() 2020年高中一年级第一学月考试
2020年高中一年级第一学月考试
数学考试试题
需要注意的地方:
1.答题前,考生务势必我们的名字和准考证号填写在答卷卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答卷卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答卷卡上。写在本![]() 试题上无效。
试题上无效。
3.考试结束后,将本试题和答卷卡一并交回。
第I卷 选择题(60分)
1、选择题:本题共12小题,每小题5分,共60分。在每小题给的四个选项中,只有一项是符合题目需要的。
1.已知区间![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知函数![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.函数![]() 的最小正周期为
的最小正周期为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知f=cosplay![]() ,则下列等式成立的 是
,则下列等式成立的 是
A.f=f B.f=f C.f=-f D.f=f
5.设![]() 是概念在
是概念在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.若角![]() 的终边过点
的终边过点![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.“龟兔赛跑”讲述了如此的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用![]() ,
,![]() 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程,![]() 为时间,则与故事情节相吻合的是
为时间,则与故事情节相吻合的是
A.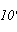 B.
B.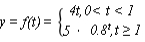 C.
C.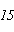 D.
D.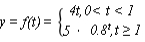
8.为了求函数![]() 的一个零点,某同学借助计算器得到自变量
的一个零点,某同学借助计算器得到自变量![]() 和函数
和函数![]() 的部分对应值,如表所示:
的部分对应值,如表所示:
| 1.25 | 1.3125 | 1.375 | 1.4375 | 1.5 | 1.5625 |
| -0.8716 | -0.5788 | -0 | 0.2101 | 0.32843 | 0.64115 |
则方程![]() 的近似解(精准到0.1)可取为
的近似解(精准到0.1)可取为
A.1.32 B.1.39 C.1.4 D.1.3
9.函数![]() 的部分图象是
的部分图象是
A.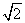 B.
B.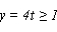 C.
C.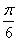 D.
D.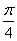
10.已知函数![]() ,则函数
,则函数![]() 的单调减区间为[来源:Zxxk.Com]
的单调减区间为[来源:Zxxk.Com]
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.概念在![]() 上的奇函数
上的奇函数![]() 以5为周期,若
以5为周期,若![]() ,则在
,则在![]() 内,
内,![]() 的解的最少个数是
的解的最少个数是
A.3 B.4 C.5 D.7
12.设![]() 是
是![]() 上的周期为2的函数,且对任意的实数
上的周期为2的函数,且对任意的实数![]() ,恒有
,恒有![]() ,当
,当![]() 时,
时, ,若关于
,若关于![]() 的方程
的方程![]() 恰有五个不相同的实数根,则实数
恰有五个不相同的实数根,则实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第II卷 非选择题(90分)
2、填空题:本题共4小题,每小题![]() 5分,共20分。
5分,共20分。
13.若幂函数![]() 的图像经过点
的图像经过点![]() ,则
,则![]() __________.
__________.
14.若![]() ,则
,则![]() __________.
__________.
15.![]() 计算
计算![]() 的值为__________.
的值为__________.
16.已知函数![]() ,若
,若![]() 有解,则m的取值范围是______.
有解,则m的取值范围是______.
解答卷:共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)已知函数![]() .
.
(1)求函数![]() 的概念域
的概念域![]() ;
;
(2)若实数![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
18.(12分)已知集合![]() .
.
(1)求![]() ;
;
(![]() 2)若
2)若![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
19.(12分)已知![]() 的最小正周期为
的最小正周期为![]() .
.
求![]() 的值,并求
的值,并求![]() 的单调递增区间;
的单调递增区间;
求![]() 在区间
在区间![]() 上的值域.
上的值域.
20.(12分)函数f(x)=Asin(2ωx+φ)(A>0,ω>0,|φ|<![]() )的部分图象如图所示
)的部分图象如图所示
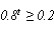 (1)求A,ω,φ的值;[来源:学.科.网]
(1)求A,ω,φ的值;[来源:学.科.网]
(2)求图中a,b的值及函数f(x)的递增区间;
(3)若α∈[0,π],且f(α)=![]() ,求α的值.
,求α的值.
21.(12分)某医药研![]() 究所开发的一种新药,假如成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量
究所开发的一种新药,假如成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量![]() (单位:微克)与时间
(单位:微克)与时间![]() (单位:小时)之间近似满足如图所示的曲线.
(单位:小时)之间近似满足如图所示的曲线.
(1)写出首次服药后![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
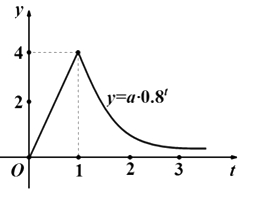 (2)据进一步测定:每毫升血液中含药量不少于
(2)据进一步测定:每毫升血液中含药量不少于![]() 微克时,治疗有效.问:服药多少小时开始有治疗成效?治疗成效能持续多少小时?(精准到
微克时,治疗有效.问:服药多少小时开始有治疗成效?治疗成效能持续多少小时?(精准到![]() ,参考数据:
,参考数据:![]() )
)
22.(12分)函数![]() 是奇函数.[来源:学|科|网Z|X|X|K]
是奇函数.[来源:学|科|网Z|X|X|K]
![]() 求
求![]() 的分析式;
的分析式;
![]()
![]() 当
当![]() 时,
时,![]() 恒成立,求m的取值范围.
恒成立,求m的取值范围.
高中一年级第一学期月考试
数学考试试题参考答案
1.A 2.C 3.C 4.D 5.A 6.C 7.B 8.C 9.B 10.C 11.D 12.D
13.![]() 14.
14.![]() 15.
15.![]() 16.
16.![]()
17.(1)要使![]() 有意义,则
有意义,则![]() 即
即![]() ,要使
,要使![]() 有意义,则
有意义,则![]() 即
即![]() 求交集即可求函数
求交集即可求函数![]() 的概念域
的概念域![]() ;
;
(2)实数![]() ,且
,且![]() ,所以
,所以![]() 即可得出
即可得出![]() 的取值范围.
的取值范围.
考试试题分析:
(1)要使![]() 有意义,则
有意义,则![]()
![]() 即
即![]()
要使![]() 有意义,则
有意义,则![]() 即
即![]()
所以![]() 的概念域
的概念域![]() .
.
(2)由(1)可得:
![]() 即
即![]() 所以
所以![]() ,
,![]() 故
故![]() 的取值范围
的取值范围![]() 是
是![]()
![]()
18.解:(Ⅰ)由![]() 得
得![]() ,即有
,即有![]()
所以![]()
![]()
![]()
令![]() 得
得![]() ,所以
,所以![]()
![]()
所以![]()
![]() .
. ![]()
(Ⅱ)由于![]() ,所以
,所以![]() ,于是
,于是![]() .
. ![]()
考试知识点:集合的运算
19.解:由![]() 的最小正周期为
的最小正周期为![]() ,得
,得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
![]() ,令
,令![]() ,则
,则![]() ,
,
![]() 的单调递增区间为
的单调递增区间为![]() ,
,
由![]() 得
得![]() ,
,
故![]() 的单调递增区间为
的单调递增区间为![]() .
.
由于![]()
![]() ,所以
,所以![]() ,
,
![]() 的取值范围是
的取值范围是![]() ,故
,故![]() 的值域为
的值域为![]() .
.
20.解:(1)由图象知A=2,![]() =
=![]() -(-
-(-![]() )=
)=![]() ,
,
得T=π,即![]() =2,得ω=1,
=2,得ω=1,
又f(-![]() )=2sin[2×(-
)=2sin[2×(-![]() )+φ]=-2,
)+φ]=-2,
得sin(-![]() +φ)=-1,
+φ)=-1,
即-![]() +φ=-
+φ=-![]() +2kπ,
+2kπ,
即![]() ω=
ω=![]() +2kπ,k∈Z,
+2kπ,k∈Z,
∵|φ|<![]() ,
,
∴当k=0时,φ=![]() ,
,
即A=2,ω=1,φ=![]() ;
;
(2)a=-![]() -
-![]() =-
=-![]() -
-![]() =-
=-![]() ,
,
b=f(0)=2sin![]() =2×
=2×![]() =1,
=1,
∵f(x)=2sin(2x+![]() ),
),
∴由2kπ-![]() ≤2x+
≤2x+![]() ≤2kπ+
≤2kπ+![]() ,k∈Z,
,k∈Z,
得kπ-![]() ≤x≤kπ+
≤x≤kπ+![]() ,k∈Z,
,k∈Z,
即函数f(x)的递增区间为[kπ-![]() ,kπ+
,kπ+![]() ],k∈Z;
],k∈Z;
(3)∵f(α)=2sin(2α+![]() )=
)=![]() ,
,
即sin(2α+![]() )=
)=![]() ,
,
∵α∈[0,π],
∴2α+![]() ∈[
∈[![]() ,
,![]() ],
],
∴2α+![]() =
=![]() 或
或![]() ,
,
∴α=![]() 或α=
或α=![]() .
.
21:(Ⅰ)依据图象知:当![]() 时,
时,![]() ;
;![]()
当![]() 时,
时,![]() ,由
,由![]() 时,
时,![]() 得
得![]() [来源:学科网]
[来源:学科网]
所以![]() ,即
,即![]()
![]()
因此![]()
![]()
(Ⅱ)依据题意知:
当![]() 时,
时,![]() ;
;![]()
当![]() 时,
时,![]()
所以![]()
![]()
所以![]() ,
,![]()
因此服药![]()
![]() 小时(即
小时(即![]() 分钟)开始有治疗成效,治疗成效能持续
分钟)开始有治疗成效,治疗成效能持续![]() 小时.
小时.![]()
22.![]() 函数
函数![]() 是奇函数,
是奇函数,
![]() ,
,
故![]() ,
,
故![]() ;
;
![]() 当
当![]() 时,
时,![]() 恒成立,
恒成立,
即![]() 在
在![]() 恒成立,
恒成立,
令![]() ,
,![]() ,
,
显然![]() 在
在![]() 的最小值是
的最小值是![]() ,故
,故![]() ,解得:
,解得:![]() .
.







