 第3讲 平行线的架构模型及综合
第3讲 平行线的架构模型及综合
命题:
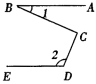
例:如图,有下列三个条件:①DE∥BC:②∠1=∠2;③∠B=∠C.
 若从这三个条件中任选两个作为题设,另一个作为结论,组成一个命题,一共能组成几个命题,请你都写出来;
若从这三个条件中任选两个作为题设,另一个作为结论,组成一个命题,一共能组成几个命题,请你都写出来;
请你就其中的一个真命题给出推理过程。
平移:
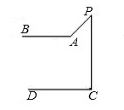
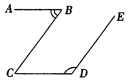
1.小明和小华在手工制作课上用铁丝制作楼梯模型如图1 所示,那样他们用的铁丝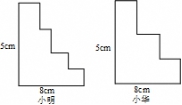
A、一样多 B、小明的多 C、小华的多 D、不可以确定
2.如图,第1个图案是由黑白两种颜色的正六边形地面砖组成,第2个,第3个图案可以看作是第1个图案经过平移而得,那样第4个图案中有白色六边形地面砖______块,第n个图案中有白色地面砖__________ 块.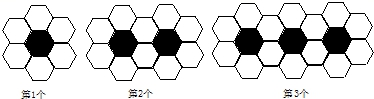
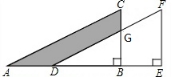
3.如图,将Rt△ABC沿AB方向平移得到Rt△DEF,已知BE=6,EF=8,CG=3,求阴影部分的面积。
探究:夹在平行线间的折线问题,平行线的架构:“铅笔”型,“M”型,过拐点作已知直线的平行线。
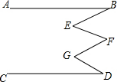
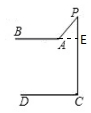
例1.已知:如图,AC∥BD,折线AMB夹在两条平行线间. 判断∠M,∠A,∠B的关系;

例2.如图所示,已知AB∥CD,分别探讨下面的四个图形中∠APC与∠PAB﹑∠PCD的关系,请你从所得关系中任意选取一个加以说明。

训练:1.如图1所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若
∠1=35°,则∠2的度数为__________.
2.如图2所示是汽车灯的剖面图,从坐落于O点灯发出光照射到凹面镜上反射出的光线BA,CD都是水平线,若∠ABO=α,∠DCO=60∘,则∠BOC的度数为( )
A.180∘−α B. 120∘−α C. 60°+α D. 60∘−α
3.如图3,AB∥CD,∠B=115°,∠C=45°,则∠BEC的度数为__________°.
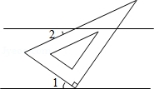 图1
图1 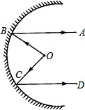 图2
图2  图3
图3
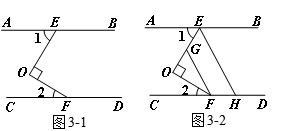
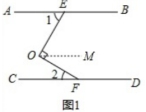
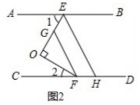
例3:如图3-1,已知:AB∥CD,点E,F分别在AB,CD上,且OE⊥OF.
(1)求证:∠1+∠2=90°;
(2)如图3-2,分别在OE,CD上取点G,H,使FO平分∠CFG,EO平分∠AEH,求证:FG∥EH.
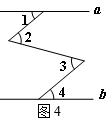
例4:如图4,a∥b,∠2=∠3,∠1=40°,则∠4的度数是__________度.
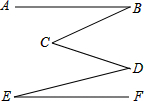
例5:如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°,求证:AB∥EF:
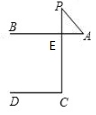
训练:1.如图AB∥CD,∠B=∠C,求证:BE∥CF。

2.如图,假如AB∥CD,CD∥EF,那样∠BCE等于
A.∠2-∠1 B.∠1+∠2 C.180°-∠2+∠1 D.180°-∠1+∠2
3.如图,AB∥CD,则下列等式成立的是( )
A. ∠B+∠F+∠D=∠E+∠G B.∠E+∠F+∠G=∠B+∠D
C. ∠F+∠G+∠D=∠B+∠E D. ∠B+∠E+∠F=∠G+∠D
4.如下图,AB∥DE,那样∠BCD=.
A.∠2-∠1 B.∠1+∠2 C.180°+∠1-∠2 D.180°+∠2-2∠1

![]()
![]()
平行线与折叠:(角度计算)
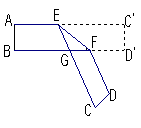
1. 一张对边互相平行的纸条折成如图所示,EF是折痕,若![]() ,则①
,则① ![]()
② ![]() ③
③![]() ④
④ ![]() 以
以![]() 上结论正确的有__________.(填序号)
上结论正确的有__________.(填序号)
 2.将一直角三角板与两边平行的纸条如图所示放置,下列结论:
2.将一直角三角板与两边平行的纸条如图所示放置,下列结论:
∠1=∠2; ∠3=∠4;
∠2+∠4=90°; ∠4+∠5=180°
其中正确的个数是.
A.1 B.2 C.3 D.4
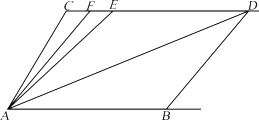
3.如图,已知射线CD∥AB,∠C=∠ABD=110°,E,F在CD上,且满足∠EAD=∠EDA,AF平分∠CAE.
(1)求∠FAD的度数;
(2)若向右平行移动BD,其它条件不变,那样∠ADC:∠AEC的值是不是发生变化?若变化,找出其中规律;若不变,求出这个比值;
(3)在向右平行移动BD的过程中,是不是存在某种状况,使∠AFC=∠ADB?若存在,请求出∠ADB度数,若没有,说明理由.
作业:
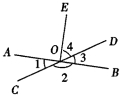
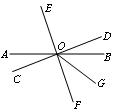
1.如图,已知直线AB、CD相交于O,OE⊥AB,∠1=25°,则∠2=______°,∠3=______°,∠4=______°.
2.如图直线l1∥l2,AB⊥CD,∠1=34°,那样∠2的度数是______.

3.王强从A处沿北偏东60°的方向到达B处,又从B处沿南偏西25°的方向到达C处,则王强两次行进路线的夹角为______度.
4.如图,AB∥CD,BC∥ED,则∠B+∠D=______.
5.如图所示,直线AB,CD,EF交于点O,OG平分∠BOF,CD⊥EF,∠AOE=70°,求∠DOG的度数.
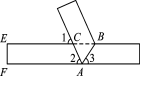
6.有一条长方形纸带,按如图所示方法沿AB折叠,若∠1=64°,求图中∠3的度数.
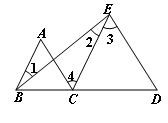
7.已知:如图所示,∠1=∠2,∠A=∠3.求证:AC∥DE
8.已知:如图,CD⊥AB于D,DE∥BC,EF⊥AB于F,求证:∠FED=∠BCD.

第3讲 平行线的架构模型及综合答案
命题:
解:一共能组成2个命题,它们是:题设:①②,结论:③;题设:①③,结论:②;
状况一题设:①②,结论:③;
证明:如图,∵DE∥BC,
∴∠1=∠B,∠2=∠C.
又∵∠1=∠2,
∴∠B=∠C;
状况二题设:①③,结论:②;
证明:如图,∵DE∥BC,
∴∠1=∠B,∠2=∠C.
又∵∠B=∠C,
∴∠1=∠2.
平移:
1.A 2. 18,4n+2 3. 39
探究:
例1.∠M+∠A+∠B=180° (2)∠M=∠A+∠B
例2.如图所示,已知AB∥CD,分别探讨下面的四个图形中∠APC与∠PAB﹑∠PCD的关系,请你从所得关系中任意选取一个加以说明。
解:
图1:∠APC=∠PAB-∠PCD
 延长BA交PC于E,
延长BA交PC于E,
∵AB∥DC,
∴∠PEA=∠C,
∵∠PAE+∠1+∠P=180,
∴∠PAE+∠PAB=180.
∴∠PAB=∠C+∠P;
图2:∠APC=∠PCD−∠PAB,
 ∵AB∥DC,
∵AB∥DC,
∴∠PEB=∠C,
∵∠PEA+∠A+∠P=180°,
∠PEA+∠PEB=180°
∴∠PEB=∠P+∠A,
∴∠APC=∠PCD−∠PAB
训练:
1. 25° 2. C 3. 110°
例3:证明:过点O作OM∥AB,
则∠1=∠EOM,
 ∵AB∥CD,
∵AB∥CD,
∴OM∥CD,
∴∠2=∠FOM,
∵OE⊥OF,
∴∠EOF=90∘,
即∠EOM+∠FOM=90∘,
∴∠1+∠2=90∘;
∵AB∥CD
 ∴∠AEH+∠CHE=180∘,
∴∠AEH+∠CHE=180∘,
∵FO平分∠CFG,EO平分∠AEH
∴∠CFG=2∠2,∠AEH=2∠1,
∵∠1+∠2=90∘
∴∠CFG+∠AEH=2∠1+2∠2=180∘,
∴∠CFG=∠CHE,
∴FG∥EH.
例4: 40
例5:过C点作CG∥AB,过点D作DH∥AB,则CG∥DH,
∵∠B=25°,
∴∠BCG=25°,
∵∠BCD=45°,
 ∴∠GCD=20°,
∴∠GCD=20°,
![]() ∵CG∥HD,
∵CG∥HD,
![]()
![]() ∴∠CDH=20°,
∴∠CDH=20°,
![]() ∵∠CDE=30°,
∵∠CDE=30°,
∴∠HDE=10°
∴∠HDE=∠E=10°,
∴DH∥EF,
∴DH∥AB,
∴AB∥EF.
训练:1.略,同例5 2.C 3. A 4.C
平行线与折叠:(角度计算)
1. ①③ 2.D
3.(1)∠FAD=35∘
∵射线CD∥AB,∠C=110°,
∴∠CAB=70°,∠BAD=∠EAD,
∵∠EAD=∠EDA,
∴∠EAD=∠BAD=![]() ∠EAB.
∠EAB.
∵AF平分∠CAE,
∴∠FAD=∠FAE+∠EAD
=![]() CAB=
CAB=![]() ×70°=35°;
×70°=35°;
(2)不变。
∵AB∥CD,∠C=110∘,
∴∠CAB=70∘.
当BD向右平移时,∠EAD增大,∠CAB不变,
∵∠EAD=∠EDA,∠AEC=∠EAD+∠EDA,
∴∠ADC:∠AEC=1:2;
(3)存在
∠BAD=∠EAD=∠EDA=x°,
∵由知∠FAD=35°,
∴∠AFC=x°+35°.
∵AB∥CD,∠ABD=110°,
∴∠BDC=70°,
∴∠ADB=70°−x°,
∵∠AFC=∠ADB,
∴x+35=70−x,
解得x=17.5,
∴∠ADB=70°−17.5°=52.5°.
作业:







