![]() 5.辅助线之架构特殊三角形
5.辅助线之架构特殊三角形
1.如图,在凯里市某广场上空飘着一只汽球![]() ,
,![]() 是地面上相距
是地面上相距![]() 米的两点,它们分别在汽球的正西和正东,测得仰角
米的两点,它们分别在汽球的正西和正东,测得仰角![]() ,仰角
,仰角![]() ,求汽球
,求汽球![]() 的高度为多少.(精准到
的高度为多少.(精准到![]() 米,
米,![]() =1.732)
=1.732)
答案:32.9
分析:
过点![]() 作
作![]() 于
于![]() 点,设
点,设![]() 米.
米.
在![]() 中,
中,![]() ,
,
∴![]() (米)
(米)
在![]() 中,
中,![]()
∴![]() (米)
(米)
又∵![]()
∴![]()
∴![]() (米)
(米)
∴![]() (米)
(米)
2.如图,在![]() 中,已知
中,已知![]() ,求
,求![]() 中
中![]() 多少度;
多少度;![]() 多少度;
多少度;![]() 多少度.
多少度.
答案:30;30;120
分析:
作![]() 于点
于点![]() ,则
,则![]() ,
,

由![]() ,得
,得![]()
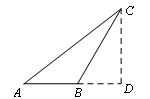
3.如图所示,天空中有一静止的广告气球![]() ,从地面
,从地面![]() 点测得
点测得![]() 的仰角为45°,从地面
的仰角为45°,从地面![]() 点测得
点测得![]() 的仰角为60°.已知
的仰角为60°.已知![]() 米,点
米,点![]() 和直线
和直线![]() 在同一铅垂平面上,求气球离地面的高度
在同一铅垂平面上,求气球离地面的高度![]() (结果保留根号).
(结果保留根号).
答案:![]()
分析:
作![]() ,垂足为
,垂足为![]() ,设气球离地面的高度为
,设气球离地面的高度为![]() 米.
米.![]()
在![]() 中,
中,![]() ,∴
,∴![]() .[来源:Zxxk.Com]
.[来源:Zxxk.Com]
在![]() 中,
中,![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
答:气球离地面的高度为![]() 米
米
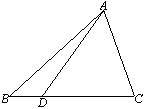
4.已知:如图,![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() ,求
,求![]() 的度数及
的度数及![]() 的长?
的长?
答案:见分析
分析:
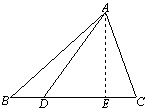
过![]() 点作
点作![]() 于
于![]()
![]() ,则
,则![]() .
.
在![]() 中,
中,![]() ,
,
∴![]()
在![]() 中,
中,![]() ,∴
,∴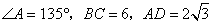 ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,∴
,∴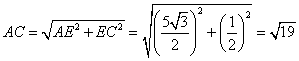
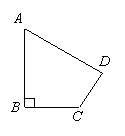
5.某旅游区有一个景观奇![]() 异的望天洞,
异的望天洞,![]() 点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭
点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭![]() 处观看旅游区风景,最后坐缆车沿索道
处观看旅游区风景,最后坐缆车沿索道![]() 返回山脚下的
返回山脚下的![]() 处.在同一平面内,若测得斜坡
处.在同一平面内,若测得斜坡![]() 的长为
的长为![]() 米,坡角
米,坡角![]() ,在
,在![]() 处测得
处测得![]() 的仰角
的仰角![]() ,在
,在![]() 处测得
处测得![]() 的仰角
的仰角![]() ,过
,过![]() 点作地面
点作地面![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
(1)求![]() 的度数;
的度数;
(2)求索道![]() 的长.(结果保留根号)
的长.(结果保留根号)
答案:见分析
分析:
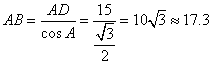
⑴∵![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴![]() .
.
⑵过点![]() 作
作![]() 于点
于点![]() .
.
在![]() 中,
中,![]() ,
,
![]() ∴
∴![]() ,[来源:Z.xx.k.Com]
,[来源:Z.xx.k.Com]
又∵![]() ,
,
∴![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() (米)
(米)
答:索道长![]() 米.
米.
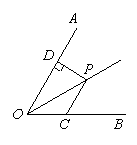
6.如图,点![]() 是
是![]() 的角平分线上一点,过点
的角平分线上一点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .若
.若![]() ,求点
,求点![]() 到
到![]() 的距离
的距离![]() .
.
答案:6
分析:

过![]() 点作
点作![]() ,并交
,并交![]() 于点
于点![]() .
.
∵![]() 是
是![]() 的角平分线,
的角平分线,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
7.某片绿地的形状如图所示,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长为_
的长为_![]() 、
、![]() 的长为___
的长为___![]() .(精准到
.(精准到![]() ,
,![]() ).
).

答案:227;146
分析:

延长![]() 、
、![]() 交于点
交于点![]() ,
,
在![]() 中,
中,![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,
,
从而![]()
![]()
![]() .
.
在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
从而![]()
![]()
![]() ,
,
∴![]()
![]()
![]() ,
,
![]()
![]()
![]() .
.
8.已知:如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .求这个四边形的面积.
.求这个四边形的面积.
答案:![]()
分析:

连结![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,![]() 是直角三角形,面积为
是直角三角形,面积为![]() ,且
,且![]() ,在
,在![]() 和
和![]() 中,设
中,设![]() ,
,![]() ,解得
,解得![]() ,
,
∴![]() ,
,![]() ,
,
∴四边形的面积为![]() .
.
9.如图,已知梯形![]() 中,
中, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则下底
,则下底![]() 的长为 ___.
的长为 ___.
答案:10
分析: 过![]() 作
作![]() ,把梯形分成平行四边形和直角三角形,借助平行四边形的对边相等得到
,把梯形分成平行四边形和直角三角形,借助平行四边形的对边相等得到![]() ,所以
,所以![]() 可以求出,在直角三角形中,依据
可以求出,在直角三角形中,依据![]() ,借助勾股定理求出
,借助勾股定理求出![]() 的长也就能求出了.
的长也就能求出了.
解:如图,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
![]() ,
,![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (直角三角形
(直角三角形![]()
![]() 角所对的直角边等于斜边的一半),
角所对的直角边等于斜边的一半),
在![]() 中,
中,![]() ,
,
即![]()
![]()
![]()
![]() ,
,
解得![]() ,
,
![]() .
.
故答案为:10.
10.如图,在鱼塘两![]() 侧有两棵树
侧有两棵树![]() 、
、![]() ,小华要测量此两树之间的距离.他在距
,小华要测量此两树之间的距离.他在距![]() 树
树![]() 的
的![]() 处测得
处测得![]()
![]() ,又在
,又在![]() 处测得
处测得![]() .求
.求![]() 、
、![]() 两树之间的距离?(结果精准到
两树之间的距离?(结果精准到![]() )(参考
)(参考![]() 数据:
数据:![]() ,
,![]() )
)

![]()
答案:17.3
分析:
作![]() ,垂足为点
,垂足为点![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
在![]() 中,∵
中,∵![]() ,∴
,∴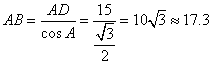 .
.
答:![]() 、
、![]() 两树之间的距离约为
两树之间的距离约为![]() .
.
11.如图,在![]() 中,
中,![]() ,则
,则![]() 的值为多少.
的值为多少.
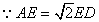
答案:4
分析:作![]() 的中线
的中线![]() ,过
,过![]() 作
作![]() 于
于![]() ,求出
,求出![]() ,求出
,求出![]() ,依据勾股定理求出
,依据勾股定理求出![]() ,代入求出即可.
,代入求出即可.
解
: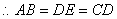
作![]() 的中线
的中线![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
由勾股定理得:![]() ,
,
![]() ,
,
![]() 在
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]()
![]() .
.
12.如图![]() ,在梯形
,在梯形![]() 中,
中,![]() ,垂足为点
,垂足为点![]() .若
.若![]() ,求
,求![]() 的长为__.
的长为__.
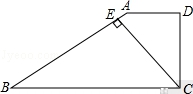
答案:2
分析:过点![]() 作
作![]() 于
于![]() ,借助锐角三角函数关系得出
,借助锐角三角函数关系得出![]() 的长,进而得出
的长,进而得出![]() 的长,再依据含
的长,再依据含![]() 角的直角三角形的性质即可得出
角的直角三角形的性质即可得出![]() 的长.
的长.
解:过点![]() 作
作![]() 于
于![]() ,则
,则![]() ,
,

在![]() 中,
中,![]() ,
,
![]() ,
,
即![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
13.如图,四边形![]() 中,
中,![]() ,且
,且![]() ,求四边形
,求四边形![]() 的面积为__.
的面积为__.
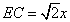 [来源:学科网ZXXK]
[来源:学科网ZXXK]
答案:1.5
分析:解:如图延长![]() 交
交![]() 延长线于点
延长线于点![]() ,
,
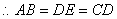
![]()
![]()
![]()
![]()
![]()
![]()
又![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 的面积
的面积![]()
14.如图,在平行四边形![]() 中,
中,![]() 分别在
分别在![]() 和
和![]() 的延长线上,
的延长线上,![]() .求
.求![]() 的长
的长

分析:第一证明四边形![]() 是平行四边形,可得
是平行四边形,可得![]() ,即
,即![]() 为
为![]() 中点,然后再得
中点,然后再得![]() ,再借助三角函数可求出
,再借助三角函数可求出![]() 和
和![]() 的长即可.
的长即可.
解:![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
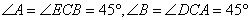
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,即
,即![]() 为
为![]() 中点,
中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
过![]() 作
作![]() 于点
于点![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
15.如图,在四边形![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为____.
的面积为____.

答案:12
分析:依据题意推知![]() 和
和![]() 是等腰直角三角形,则
是等腰直角三角形,则![]() .
.
解:如图,延长![]() 交于点
交于点![]() .
.
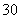
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故答案是:12.
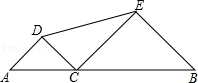
16.某校在一块如图所示的三角形空地上种植某种草皮以美化环境,已知这种草皮每平米![]() 元,则购买这种草皮至少要__________元.
元,则购买这种草皮至少要__________元.
![]()
答案:150a
分析:先做![]() 的高
的高![]() ,求出
,求出![]() ,再得出
,再得出![]() ,再依据
,再依据![]() 求出三角形的面积,最后依据这种草皮每平米
求出三角形的面积,最后依据这种草皮每平米![]() 元,即可得出答案.
元,即可得出答案.
解:做![]() 的高
的高![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 这种草皮每平米
这种草皮每平米![]() 元,
元,
![]() 购买这
购买这![]() 种草皮至少要
种草皮至少要![]() 元,
元,
故答案为:150a.
17.如图,四边形![]() 中,
中,![]() ,则
,则![]() 的长
的长

分析:延长![]() 交于
交于![]() ,求出
,求出![]() ,求出
,求出![]() 长,在
长,在![]() 中,求出
中,求出![]() ,在
,在![]() 中,依据勾股定理求出
中,依据勾股定理求出![]() 即可.
即可.![]()
解: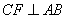
延长![]() 交于
交于![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,由勾股
中,由勾股![]() 定理得:
定理得:![]() .
.
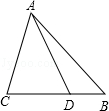
18.如图,在![]() 中,
中,![]() 交边
交边![]() 于点
于点![]()
(1)求![]() 的度数为__
的度数为__![]() ;
;
(2)求![]() 的度数为___.
的度数为___.
答案:45;45
分析:(1)依据已知可求得![]() 的度数,再依据三角形外角的性质即可求得
的度数,再依据三角形外角的性质即可求得![]() 的度数.(2)过
的度数.(2)过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,依据直角三角形中
,依据直角三角形中![]() 度所对的边是斜边的一半及已知可推出
度所对的边是斜边的一半及已知可推出![]() ,从而可得到
,从而可得到![]() ,从而可求得
,从而可求得![]() ,依据等角对等边可得
,依据等角对等边可得![]() ,再借助等边对等角的性质即可证得结论.
,再借助等边对等角的性质即可证得结论.
(1)解:![]() ,
,
![]() ,
,
![]() ;[来源:学_科_网Z_X_X_K][来源:学,科,网Z,X,X,K]
;[来源:学_科_网Z_X_X_K][来源:学,科,网Z,X,X,K]
(2)证明:过![]() 作
作![]() 于
于![]() ,连接
,连接![]() .
.
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
19.如图,在五边形![]() 中
中![]() ,则五边形
,则五边形![]() 的周长是()
的周长是()
分析:可延长![]() 和
和![]() 交于一点
交于一点![]() ,依据正方形的性质和等腰直角三角形的性质即可求出
,依据正方形的性质和等腰直角三角形的性质即可求出![]() 和
和![]() 的值,进而求出答案.
的值,进而求出答案.
解:可延长![]() 和
和![]() 交于一点
交于一点![]() ,
,
依据五边形的内角和定理和已知条件,可得![]() 是等腰直角三角形,四边形
是等腰直角三角形,四边形![]() 是正方形.
是正方形.
则![]() ,∴
,∴![]()
所以五边形的周长是![]() .
.
20.如图,四边形![]() 中,
中,![]() ,则
,则![]() 的长为
的长为
分析:延长![]() ,两延长线相交于点
,两延长线相交于点![]() ,依据
,依据![]() 是等腰直角三角形,得
是等腰直角三角形,得![]() ,从而求出
,从而求出![]() 的长.
的长.
解:如图,延长![]() ,两延长线相交于点
,两延长线相交于点![]() ,
,

![]() ,
,
![]() 是等腰直角三角形
是等腰直角三角形
![]() ,又
,又![]()
![]() 是等腰直角三角形
是等腰直角三角形
设![]() ,则
,则![]()
![]()
![]()
![]()
解得:![]()
21.如图,线段![]() 的长为
的长为![]() ,
,![]() 为
为![]() 上一个动点,分别以
上一个动点,分别以![]() 为斜边在
为斜边在![]() 的同侧作两个等腰直角三角形
的同侧作两个等腰直角三角形![]() 和
和![]() ,那样
,那样![]() 长的最小值是____.
长的最小值是____.

答案:1
分析:依据垂线段最短这个要点来架构辅助线解题.
解:延长![]() 和
和![]() 交于一点
交于一点![]() ,连接
,连接![]()

∵![]() 和
和![]() 均为等腰直角三角形
均为等腰直角三角形
∴![]()
∴![]()
∴四边形![]() 为矩形
为矩形
∴![]()
∵当![]() 时,
时,![]() 有最小值。且
有最小值。且![]() 为等腰直角三角形
为等腰直角三角形
∴![]() 的最小值
的最小值![]()
∴![]() 的最小值为1
的最小值为1







