上师大附中闵行分校高中三年级第一学期首次月考
数学试题
填空题
1.设全集
______.
2.不等式
的解集为______.
3.已知
的值为_______.
4.方程
的解
=______.
5.设函数
_______.
6.函数
的反函数为
______.
7.设
若函数
是偶函数，则
的单调递增区间是_______.
8.若面积的最大最是______.
9.已知
，若对任意实数
的最小值为______.
10.已知直线交于点
则不等式
的解集为_____.
11.已知概念域为的函数
满足
函数
函数
零点的个数是______.
12.已知点
，且平行四边形
的四个顶点都在函数的图像上，设
为原点，已知三角形的面积为
，则平行四边形的面积为_____.
2、选择题
13.下列说法中正确的是（ ）
A．命题“若，则
”的否命题是“，则”
B．“
”是“”的必要不充分条件
C．命题“若
”的逆否命题是真命题
D．“
的充分非必要
14.解不等式时，可架构函数
，由是减函数，及
，可得
，用类似的办法可求得不等式
的解集为（ ）
A． B．
C．
D．
15.已知是概念在上的增函数，函数的图像关于点
对称，若实数
满足等式
的取值范围是（ ）
A．
B． C． D．
16.若存在实数
，对任意实数，使不等式恒成立，则
的取值范围为（ ）
A．
B．
C． D．
3、解答卷
17.已知全集
，集合
18．已知函数
（1）求的单调区间
（2）解不等式
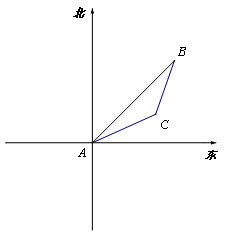
19．在一个特定时段内，以点D为中心的7海里以内海域被设为警戒水域。点D正北55海里处有一个雷达观测站A。某时刻测得一艘匀速直线行驶的船只坐落于点A北偏东45°且与点A相距海里的地方B处，经过40分钟又测得该船已行驶到点A北偏东45°+（其中
）且与点A相距
海里的地方C处。
（1）求该船的行驶速度（单位：海里/小时）；
（2）若该船不改变航行方向继续行驶，判断它会不会进入警戒水域，并说明理由。
20.已知函数
（1）当时，解关于的不等式
（2）对于给定的正数,有一个最大的正数,使得在整个区间上，不等式
恒成立，求出的分析式。
（3）函数
的最大值为0，最小值是-4，求实数和的值。
21.若函数满足：对于任意正数,都有，则称函数为
函数
（1）试判断函数
是不是是函数
（2）若函数为函数，求实数的取值范围
（3）若函数为函数，且，求证：对任意，都有
