曹杨二中2018-2019学年度第一学期高二期末数学复习试题1
1、填空题
1.直线
和平面
相交于点A,用集合符号表示_________.
2.△ABC所在平面外一点P到三角形三个顶点距离相等,那样P在内的射影肯定是△ABC的_______.
3.半径为2的球的表面积为________.
4.已知圆锥的底面半径为3,体积为12π,则圆锥侧面积为________.
5.已知地球的半径为R，在北纬45°东经30°有一座城市A，在北纬45°西经60°有一座城市B，则坐飞机从A城市到B城市的最短距离为_______.
6.设表示平面,
表示直线,给定下列四个命题：
①
②
③
④
其中正确的命题的是___________.
7.已知点P是棱长为1的正方体的底面
上一点，则
的取值范围是_________.
8.半径为R的两个球,其中一个球的球心在另一个球的球面上,则两球的交线长为_____.
9.已知正四棱锥的棱长都相等,侧棱PB、PD的中点分别为M、N,则截面AMN与底面ABCD所成的二面角的余弦值是___________.
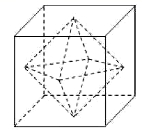
10.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.
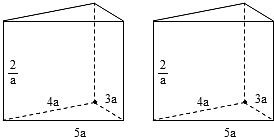
11.有两个相同的直三棱柱，高为
底面三角形的三边长分别为
则它们拼成一个三棱柱或四棱柱，在所大概的情形中，全方位积最小的个四棱柱，则
的取值范围是
___________.
12.平面过正四棱柱的顶点A，底面边长为3，侧棱长为4，∥平面
平面
平面
则
所成角的余弦值为_______.
2、选择题
17.如图，三棱柱中
，它的体积是
底面△ABC中，∠BAC=90°，AB=4，AC=3，B在底面的射影是D，且D为BC的中点。
求侧棱与底面ABC所成角的大小；
求异面直线与
所成角的大小.
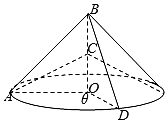
18.如图，等腰直角△AOB，OA=OB=2，点C是OB的中点，△AOB绕BO所在的边逆时针旋转一周.
求△ABC旋转一周所得旋转体的体积V和表面积S；
设OA逆时针旋转至OD，旋转角为且满足AC⊥BD，求
19.如图,四边形ABCD和ABEF均为边长为1的正方形,且二面角C-AB-E的大小为
求点B到平面ACE的距离；
求异面直线AE和BD所成角的大小。
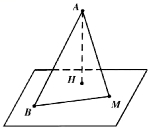
20.如图,某风景区有空中景点A及地面景点B，已知AB与地面所成角的大小为60°，点A在地面上的射影为H.
若C在地面上,且AC与底面所成角的大小为45°,求
的值；
请在地面上找一点C,使得
达到最大值.
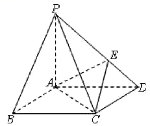
21.如图，在底面是菱形的四棱锥中，PA⊥底面ABCD，PA=AC=2，∠ABC=60°，点E在线段PD上，且PE:ED=2:1.
求证:AB与CE为异面直线；
求二面角
的大小；
在棱PC上是不是存在一点F,使得BC∥平面AEC?证明你的结论。
