上海2020-2021学年三林中学高中一年级上学期数学期中考试
命题人：蒲红军 2018年11月
1、填空题（本大题共12题，满分36分，每小题对得3分，不然一律不能分）
1.用列举法表示集合
为__________________.
2.设集合
，若
，则满足该条件的
共有__________
3.已知命题：若“
，则
”，则该命题的等价命题为_______
4.设函数
，则
的概念域为___________
5.已知
，，则
________
6.已知集合
只含有一个元素，则实数
的值是___________
7.已知全集
，则
______________
8.设
，
，若
是
的充分条件，则实数的取值范围为____________
9.已知关于
的不等式
的解集为
，若
且
，则实数的取值范围是____________.
10.对任意两个集合
，称为的对称差，概念
。设
，则
____________
11.设关于的不等式
的解集是R，则实数的取值范围为_____
12.若关于的不等式解集非空，则实数的取值范围是___________
2、选择题（本大题共4题，满分12分，每题有且只有一个正确答案，选对得3分，不然一律不能分）
13.下列图形是函数图象的是（ ）
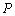
14.已知，那样下列命题正确的是（ ）
A.
B.
C. D.
15.对任意实数
，下列命题中，真命题是（ ）
A.“
”是“”的必要条件
B.“
”是“
”的必要条件
C.“”是“”的充分条件
D.“”是“”的充分条件
16.满足的集合与
共有（ ）
A.4组 B.6组 C.9组 D.11组
3、解答卷：（本大题共有6题，满分52分，每题需要写出必要的解题步骤）
17.（本题6分）
已知，比较
与的大小.
解：
18.（本题8分）
解不等式组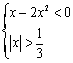
19.（本题满分8分，（1）题4分，第（2）题4分）
已知
，
（1）若
，求
；
（2）若
，求实数的取值范围.
解：
20.（本题满分8分，第（1）题4分，第（2）题4分）
设集合
，又，
，
（1）求实数的值及集合B
（2）求实数的值.
21.（本题满分12分，第（1）题8分，第（2）题4分）
某公司一年需购买某种材料400吨，设公司每次都购买吨，每次运费为4万元，一年的总存储成本为
万元.
（1）要使一年的总运费与总存储成本之和最小，则每次购买多少吨？
（2）要使一年的总运费与总存储成本之和低于200万元，则每次购买量在什么范围？
解：
22.（本题满分10分，第（1）题4分，第（2）题6分）
已知关于的不等式组
（1）求解不等式（B）的解集
（2）若不等式组的整数解集M中有且只有一个元素，求实数
的取值范围及相应的集合M.
解：
