七宝中学高中三年级上期中
1、 填空题
1. 计算：
__________
2. 对于任意
，
，函数
的图像总过一个定点，这个点的坐标是__________
3. 函数
的最小正周期是__________
4. 已知集合
，
的
文氏图如图所示，图中阴影部分表示集合A、B的某种
运算结果（用P表示），则集合
__________
5. 设函数
，则函数的概念域是__________
6. 已知函数
和
的概念如下表：
则方程
的解集是__________
7. 已知函数
的值域是
，其中
，则满足条件的有序实数
对
共有__________对
8. 已知等差数列
的前n项和为
，且，
，当时，数列
满足
，若，则n的最小值为__________
9. 已知，
，且a、ab、b成等差数列，则
__________
10. 若函数
的值域为
，则
__________
11. 关于x的不等式
的解集为，则__________
12. 概念在
上的函数满足对任意，
成立，当时，
，则在
内，函数的所有零点之和为__________
2、 选择题
13. 下列图形表示数集D到C的对应法则，其中表示概念域是D，值域是C的函数的是（ ）
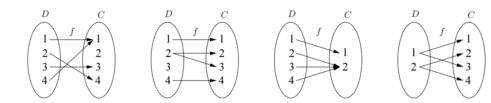
A. B. C. D.
14. 若一段圆弧的长等于该圆内接正方形边长，则这段弧所对圆心角的弧度数为（ ）
A. 
B. C. D. 
15. 若为奇函数，且是的一个零点，则下列函数中，
肯定是其零
点的函数是（ ）
A. B.
C. D. 
16. 已知数列中，
，将数列中的整数项按原来的顺序组成
数列，则（ ）
A. 5035 B. 5039 C. 5043 D. 5047
3、 解答卷
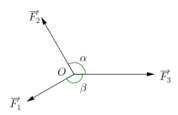
17. 在一个平面内，一质点O受三个力、、
有哪些用途维持平衡，其中与的夹角
为，与的夹角为.
（1）若，
，牛，求力、的大小；
（2）若，求与满足的关系.
18. 在平面直角坐标系xOy中，动点E到定点和定直线
的距离相等.
（1）求动点E的轨迹C的方程；
（2）设动直线
与曲线C有唯一的公共点P，与直线相交于点Q，
若，求证：点M的轨迹恒过定点.
19. 已知对于任意
，函数与
的图像
在上都有三个不同交点.
（1）写出
的分析式，并求函数的最大值及此时的x的取值；
（2）若函数在
和
上单调递增，在上单调递减，
且，求
的所大概值.
20. 假如存在常数a，使得数列满足：若x是数列中的一项，则
也是数列中的一项，称数列为“兑换数列”，常数a是它的“兑换系数”.
（1）若数列2、3、6、m是“兑换系数”为a的“兑换数列”，求m和a的值；
（2）已知有穷等差数列的项数是，所有项之和是B，求证：数列是“兑换数列”，并用和B表示它的“兑换系数”；
（3）对于一个不少于3项，且各项皆为正整数的递增数列，是不是大概它既是等比数列，又是“兑换数列”？给出你的结论，并说明理由.
21. 已知函数.
（1）若函数是函数
的反函数，解方程
；
（2）当
时，概念
，设，数列的前n项和为，求
及
；
（3）对于任意，其中，当能作为一个三角形的三边长时，
也总能作为一个三角形的三边长，试探究M的最小值.
参考答案
1、 填空题
1. 
2. 3. 
4. 5.
6. 
7. 8. 9. 
10. 0 11. 12.
2、 选择题
13. C 14. D 15. B 16. C
3、 解答卷
17.（1），
；（2）
，
，
.
18.（1）；（2）略.
19.（1）
，，最大值2，，；
（2），.
20.（1），；（2）证明略，；（3）不可能；
21.（1）；（2）
；（3）最小值为2.
