作业设计
教 材 上海九年义务教育课本 初一 第一学期 (试用本)
课 题 10.5可以化为一元一次方程的分式方程
一.课堂训练
试 题 | 解 答 | 设计意图 |
A组: 1.下列方程中,那些是分式方程?(课本P85/1) (3) (4)
| 解:(2)(4)这类方程的分母中含有未知数,所以它们是分式方程.
. |
理解分式方程的意义.
|
2.解方程:(课本P85/2) (1)
(2)
(3)
(4) | 解: (1)方程两边同乘以
化简得 检验,将 左侧= 所以
(2)方程两边同乘以
移项,化简得 检验,将 左侧= 所以
(3)方程两边同乘以
移项,化简得 检验,将 左侧= 所以
(4)整理方程 方程两边同乘以
去括号,得 移项,化简得 检验,将 左侧= 所以
|
明确解分式方程的一般步骤: 1、去分母,将分式方程化为整式方程; 2、解整式方程; 3、检验所得解是不是为原方程的根.
|
3. (1)
(2)
(3)
|
剖析:要判断 解: | 理解分式方程的解的意思.
|
B组:(课本P85/4) 小丽、小明训练打字,小丽比小明每分钟多打35个字,小丽打400个字的时间与小明打300个字的时间相同,问小丽、小明每分钟分别可打多少字?
|
剖析:本题等量关系 1、小丽每分钟打字个数=小明每分钟打字个数+35 2、小丽打400个字的时间=小明打300个字的时间相同 解:设小明每分钟打 依据题意,得
方程两边同乘以
移项,化简得 经检验, 当 答:小丽每分钟打140个字,小明每分钟打105个字.
|
明确列分式方程解应用题的一般步骤: 1、剖析题意,找到等量关系; 2、设未知数、列分式方程;3、解方程; 4、两步检验; 5、写答句.
|
二.课后作业
试 题 | 解 答 | 设计意图 |
A组: 1.现有下列方程: (1) (2) (3) 其中分式方程有 (A)1个;(B)2个;(C)3个;(D)4个. | 解:依据分式方程的意义可知 得 (1) 是分式方程
所以选(B). |
进一步理解分式方程的意义.
|
2.检验 (1) (3) |
解:剖析:要判断 解: |
理解分式方程的解的意思.
|
3.解方程: (1)
(3)
(4)
| 解:(1)方程两边同乘以
去括号,得 移项,化简得 检验,将 左侧= 所以
(2)方程两边同乘以
去括号,得 移项,化简得 检验,将 左侧= 所以
(3)整理方程
方程两边同乘以
去括号,得 移项,化简得 检验,将 左侧= 所以
(4)方程两边同乘以
移项,化简得 检验,将 左侧= 所以
|
进一步明确解分式方程的一般步骤: 1、去分母,将分式方程化为整式方程; 2、解整式方程; 3、检验所得解是不是为原方程的根.
|
B组: 1. 通信员要从营地前往相距2400米的哨所去送信,然后立即按原路返回,如此出发到回到营地共花了40分钟.若通信员去送信时的速度是回来时的速度的1.5倍,求他去送信时的速度.
2.小丽和小杰一块做速算训练,小杰每分钟可以比小丽多做4道题,结果在相同的时间里,小杰做了240道速算题,而小丽只做了160道.小丽每分钟可以做多少道速算题?
| 剖析:本题等量关系 1、通信员去送信时的速度=通信员回来时的速度的1.5倍 2、通信员去送信时间+通信员回到营地时间=40分钟 解:设通信员送信回来时的速度为每分钟 依据题意,得
方程两边同除以40,得
方程两边同乘以
移项,化简得 经检验, 当 答:通信员去送信时的速度为每分钟150米.
剖析:本题等量关系 1、小杰每分钟做题数目=小丽每分钟做题数目+4 2、小杰做240道速算题的时间=小丽做160道速算题的时间 解:设小丽每分钟可以做 依据题意,得
方程两边同除以80,得
方程两边同乘以
移项,化简得 经检验, 当 答:小丽每分钟可以做8道速算题.
|
进一步明确列分式方程解应用题的一般步骤: 1、剖析题意,找到等量关系; 2、设未知数、列分式方程;3、解方程; 4、两步检验; 5、写答句.
|
|
|
|




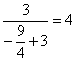 =右侧.
=右侧. 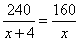 =右侧.
=右侧. 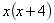 =右侧.
=右侧. 


