《4.1 几何图形》基础训练
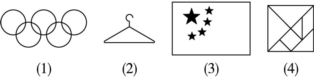
1.奥运会标志改进的图案如下,其中五环的每个环的形状与类似.
A.三角形 B.正方形 C.圆 D.长方形
2. 与红砖、足球相类似图形是.
A.长方形、圆 B.长方体、圆
C.长方形、球 D.长方体、球
3. 下列几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱。其中是立体图形的是.
A、③ ⑤ ⑥ B、① ② ③ C、③ ⑥ D、④ ⑤
4. 下列几何体中,全是由曲的面围成的是.
A.圆锥 B.正方体 C.圆柱 D.球
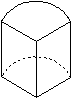
5. 下列几何图形中,是圆锥的是.

6. 下列物体的形状像球的是.
A.乒乓球 B.羽毛球 C.茶杯 D.白炽灯泡
7. 与易拉罐类似的几何体是.
A.圆锥 B.圆柱 C.棱锥 D.棱柱
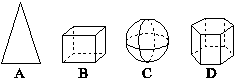
8. 下列立体图形中,是多面体的是.
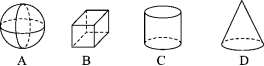
9. 将长方形绕它的一条边所在的直线旋转一周,形成的几何体是.
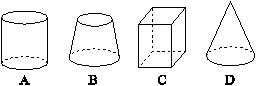
10. 下列图形中是平面图形的是.
11. 由日常的物体抽象出几何图形,在后面横线上填出对应的几何体.
铁棒__________;挂衣橱__________;魔方__________;漏斗__________;气球__________.
12. 在乒乓球、橄榄球、足球、羽毛球、冰球中,是球体的有__________.
13. 对于棱柱和圆柱:面有曲面的是_________,有平面的是_________;线有曲线的是_________,只有直线的是_________.
14. 如图,察看下列图形,并回答问题.
![]()
分别写出它们的名字:1_______;2_______;3_______;4_______;5_______.
是多面体的是_______.
15. 察看下面的各图,说出它们分别包括什么平面图形.
答案和分析
【答案】
1. C 2. D 3. A 4. D 5. B
6. A 7. B 8. B 9. A 10. A
11. 圆柱长方体正方体圆锥 球
12. 乒乓球、足球
13. 圆柱 棱柱和圆柱 圆柱 棱柱
14. 长方体 圆柱 棱柱 圆锥 球
1和3
15. 中有圆;中有三角形;中有长方形和五角星;中有正方形、三角形、平行四边形等.
【分析】
1. 解:五环的每个环的形状与圆类似,
故选C.
此题考查的是对圆的认识,五环的每个环的形状与圆类似.
2. 解:依据长方体、球的特点可知,与红砖、足球相类似图形是长方体、球,
故选D.
此题考查的是对长方体和球的认识,与红砖、足球相类似图形是长方体、球.
3. 解:下列几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱.其中是立体图形的是③⑤⑥,是平面图形的是①②④,
故选A.
此题考查的是平面图形与立体图形有什么区别. 几何图形中,像直线、角、三角形、圆等,它们上面的各点都在同一个平面内,如此的图形叫做平面图形;像长方体、圆柱体、球等,它们上面的各点不都在同一个平面内,如此的图形叫做立体图形.
4. 解:下列几何体中,全是由曲的面围成的是球,
故选D.
包围着体的是面.面有平的面与曲的面两种.长方体、四面体等,围成它们的面都是平面的一部分,如此的几何体都是多面体.圆柱、圆锥、球等都是旋转体.围成圆柱、圆锥的面有平面和曲的面,其中平的面是底面、曲的面是侧面.围成球的面是曲的面.
5. 解:A是正方体,B是棱锥,C是球,D是圆锥,
故选B.
此题考查的是对立体图形的认识,能依据立体图形的特点,分辨出不一样的立体图形是解题的重点.
6. 解:物体的形状像球的是乒乓球,
故选A.
此题考查的是对球的认识,解题重点是学会球的特点.
7. 解:与易拉罐类似的几何体是圆柱,
故选B.
此题考查的是对圆柱的认识,解题重点是学会圆柱的特点.
8. 解:球、圆柱、圆锥是旋转体,长方体是多面体,
故选B.
长方体、四面体等,围成它们的面都是平面的一部分,如此的几何体都是多面体.依据多面体的概念进行判断即可.
9. 解:将长方形绕它的一条边所在的直线旋转一周,形成的几何体是圆柱,
故选A.
此题考查的是图形绕着实线旋转一周,能形成一个哪种几何体. 明确立体图形的特点和形成过程是解题重点.
10. 解:三角形是平面图形,正方体、球、棱柱是立体图形,
故选A.
依据平面图形和立体图形的概念进行判断即可.
几何图形中,像直线、角、三角形、圆等,它们上面的各点都在同一个平面内,如此的图形叫做平面图形;像长方体、圆柱体、球等,它们上面的各点不都在同一个平面内,如此的图形叫做立体图形.
11. 解:依据立体图形的特点可知:铁棒,挂衣橱,魔方,漏斗,气球,对应的几何体分别为圆柱,长方体,正方体,圆锥,球.
故答案为圆柱;长方体;正方体;圆锥;球.
此题考查的是对立体图形的认识,能分辨出不一样的立体图形是解题的重点.
12. 解:在乒乓球、橄榄球、足球、羽毛球、冰球中,是球体的有乒乓球、足球,
故答案为乒乓球、足球.
此题考查的是对球的认识,学会球的特点是解题的重点.
13. 解:对于棱柱和圆柱:面有曲面的是圆柱,有平面的是棱柱和圆柱;线有曲线的是圆柱,
只有直线的是棱柱.
故答案为圆柱,棱柱和圆柱;圆柱,棱柱.
此题考查的是棱柱和圆柱的特征,学会棱柱和圆柱的线、面的特点是解题重点.
14. 解:察看图形,
分别写出它们的名字:
1.长方体;2.圆柱;3.棱柱;4.圆锥;5.球;
是多面体的是1和3.
长方体、四面体等,围成它们的面都是平面的一部分,如此的几何体都是多面体. 依据立体图形的特点,写出对应的立体图形的名字即可; 依据多面体的特点进行判断即可.
15. 解:中有圆;中有三角形;中有长方形和五角星;中有正方形、三角形、平行四边形等.
此题考查的是对平面图形的认识,察看各图,找出其中包括的平面图形即可.
《4.1 几何图形》提升训练
1. 下列说法正确的是.
①教科书是长方形;②教科书是长方体,也是棱柱;③教科书的表面是长方形.
A.①② B.①③ C.②③ D.①②③
2. 下列图形中,表示立体图形的个数是.
![]()
A.2 B.3 C.4 D.5
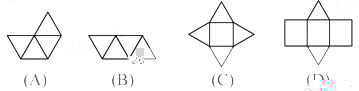
3. 下列四个图中,是三棱锥的表面展开图的是.
4. 下列图形中不是棱锥的是.

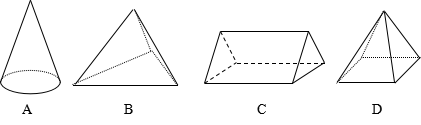
5. 下列几何体从正面看不是三角形的是.
6. 如右图所示的长方体,从不一样的方向看得到的图形是.
(A)三个相同的长方形
![]() (B)三个不相同的长方形
(B)三个不相同的长方形
(C)三个长方形中两个相同
(D)两个长方形和一个正方形
7. 下图中所示几何体从左面看到的是.

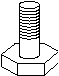
8. 如图所示,电镀螺杆呈现出了两个几何体的组合,则这两个几何体分别是______________.
9. 察看长方体和正方体模型,比较它们的相同点和不同的地方:
相同点:它们都有_________个面,_________条棱,_________个顶点;
不同的地方:长方体的6个面都是_________形,也会有2个面是_________形,它的_________面一模一样;正方体的6个面都是_________形,6个面的面积_________.
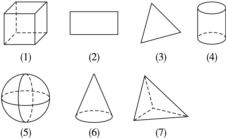
10. 下图中什么图形是立体图形,什么是平面图形?是立体图形的,写出其名字.
答案和分析
【答案】
1. C 2. B 3. B 4. A 5. C 6. B 7. A
8. 圆柱和棱柱
9. 6 12 8
长方 正方形 对 正方 面积
10. 是立体图形;是平面图形.
【分析】
1. 解:教科书是长方体,也是棱柱,故①错误,②正确;
教科书的表面是长方形,故③正确,
则说法正确的是②③,
故选C.
此题考查的是对立体图形的认识,教科书是长方体,也是棱柱,它的表面是长方形.
2. 解:圆锥、棱柱、圆柱是立体图形,其它是平面图形,故立体图形的个数是3,
故选B.
依据平面图形和立体图形的概念进行判断即可.
几何图形中,像直线、角、三角形、圆等,它们上面的各点都在同一个平面内,如此的图形叫做平面图形;像长方体、圆柱体、球等,它们上面的各点不都在同一个平面内,如此的图形叫做立体图形.
3. 解:三棱锥的表面展开图的是选项B中的图形,
故选B.
本题主要考查空间想象能力,平常多动手操作,练习是培养空间想象能力的重点,此题动手操作即可解决.
4. 解:依据棱锥的特点可知,B、C、D都是棱锥,而A是棱柱,
故选A.
此题考查的是对棱锥的认识,学会棱锥的特点是解题重点.
5. 解:选项C从正面看是长方形,
故选C.
此题考查的是对几何体的面的认识,注意是从正面看几何体所看到的图形.
6. 解:如右图所示的长方体,它的长、宽、高都不相等,故从不一样的方向看得到的图形是三个不相同的长方形,
故选B.
此题考查的是对几何体的面的认识,应该注意察看这个长方体的长、宽、高是不是相等,从而看出从不一样的方向看得到的图形是哪种.
7. 解:从左面能看到几何体的两个面,
故选A.
此题考查的是对几何体的认识,从左面察看几何体,可以看到两个面.
8. 解:电镀螺杆呈现出了两个几何体的组合,则这两个几何体分别是圆柱和棱柱,
故答案为圆柱和棱柱.
此题考查的是从实质物体中抽象出立体图形,电镀螺杆呈现出了圆柱和棱柱这两个几何体的组合.
9. 解:察看长方体和正方体模型,它们的相同点和不同的地方有:
相同点:它们都有6个面,12条棱,8个顶点;
不同的地方:长方体的6个面都是长方形,也会有2个面是正方形,它的对面一模一样;正方体的6个面都是正方形,6个面的面积相等.
故答案为6,12,8;长方,正方形,对;正方,面积.
此题考查的是正方体和长方体有什么区别,学会正方体和长方体的特点是解题重点.
10. 解:是立体图形;是平面图形.
是由6个面组成的,所以它是一个立体图形,即一个正方体.
是由1个面组成的,是一个平面图形,即长方形.
是由1个面组成的,是一个平面图形,即三角形.
是由3个面组成的,两个平面一个曲面,是一个立体图形,即圆柱体.
是由1个曲面组成的,是一个立体图形,即球体.
是由1个曲面和一个平面组成的,是一个立体图形,即圆锥体.
是由4个平面组成的,是一个立体图形,即三棱锥.
《4.1 几何图形》培优训练
1. 下列说法正确的是.
A、将长方形绕一边旋转一周可得到长方体
B、将直角三角形绕一直角边旋转一周可得到圆锥
C、将直角梯形绕一腰旋转一周可得到圆柱
D、将圆旋转一周可得到一球体
2. 将三角形绕直线L旋转一周,可以得到如下图所示立体图形的是.

① ② ③ ④
A.① B.② C.③ D.④
3. 从四面体的一个顶点发出的棱有.
A.3条 B.4条 C.5条 D.6条
4. 如图,这个几何体是由几个面组成的?面与面相交形成几条线?其中有几条线是曲的?

5. 如图是一个长方体的展开图,每一个面上都标注了字母,请依据需要回答问题:
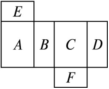
假如面A在多面体的上面,那样哪一面会在下面?
假如面F在多面体的后面,从左面看是面B,那样哪一面会在上面?
从右面看是面A,从上面看是面E,那样哪一面会在前面?
答案和分析
【答案】
1. B 2. B 3. A
4. 它是由5个面组成的,面与面相交形成9条线,其中有2条线是曲的.
5. 假如面A在多面体的上面,那样面C会在下面;
假如面F在多面体的后面,从左面看是面B,那样向外折时面C会在上面,向里折时面A会在上面;
从右面看是面A,从上面看是面E,那样向外折时以前面看是面B,向里折时以前面看是面D.
【分析】
1. 解:将长方形绕一边旋转一周可得到圆柱,故选项A错误;
将直角三角形绕一直角边旋转一周可得到圆锥,故选项B正确;
将直角梯形绕一腰旋转一周不可能得到圆柱,故选项C错误;
将圆绕一直径旋转一周可得到球体,故选项D错误;
故选B.
此题考查的是图形绕着实线旋转一周,能形成一个哪种几何体. 明确立体图形的特点和形成过程是解题重点.
2. 解:将图②中的三角形绕直线L旋转一周,可以得到如图所示的立体图形.
故选B.
将直角三角形绕一直角边旋转一周可得到圆锥,故将图②中的三角形绕直线L旋转一周,可以得到如图所示的立体图形.
3. 解:从四面体的一个顶点发出的棱有3条,
故选A.
此题考查的是对四面体的认识,从四面体的一个顶点发出的棱有3条.
4. 解:它是由5个面组成的,面与面相交形成9条线,其中有2条线是曲的.
此题考查的是几何体与点、线、面之间的关系,面与面相交成线,线与线相交成点,即:面动成体、线动成面,点动成线.
5. 解:假如面A在多面体的上面,那样面C会在下面.
假如面F在多面体的后面,从左面看是面B,那样向外折时面C会在上面,向里折时面A会在上面.
从右面看是面A,从上面看是面E,那样向外折时以前面看是面B,向里折时以前面看是面D.
解决此类问题,最好是自己做一个模型,亲手折叠一下,既生动形象,又记忆深刻.
要弄清立体图形与其平面展开图各部分间的关系,需要较强的空间想象能力,这种能力是打造在动手操作、认真察看与擅长考虑的基础上的.







